Demos and preliminary results

Problem settings

Solving heat equation with neural network:

In this problem, we learn the neural network to solve for the temperature $u$ given arbitrary conductivity field $\kappa$. The 2D heat equation is written as follows

\[\begin{aligned} -\nabla \cdot \left .( {e^\kappa \nabla u} \right.) & = f \quad \text{in } \Omega = \left .[ {0,1}^2 \right.]\\ u & = 0 \quad \text{ on } \Gamma^{\text{ext}} \\ \textbf{n} \cdot \left.({e^\kappa \nabla u}\right.) & = 0 \quad \text{ on } \Gamma^{\text{root}}, \end{aligned}\]

Results: comparison of solutions by Firedrake and TorchFire neural network

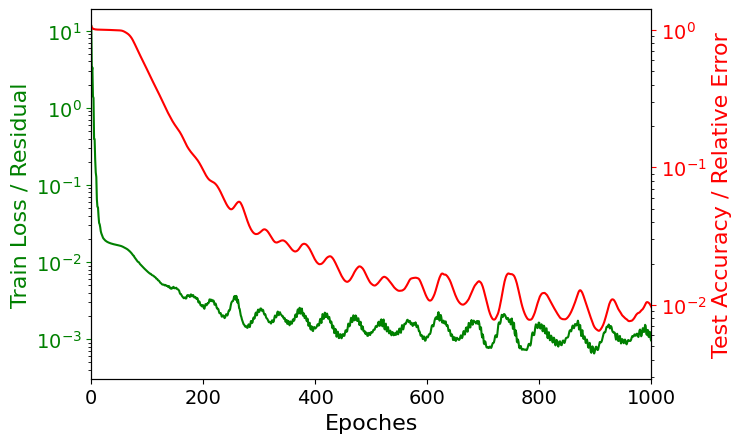
Figure 1: Training loss and test accuracy versus the training epochs

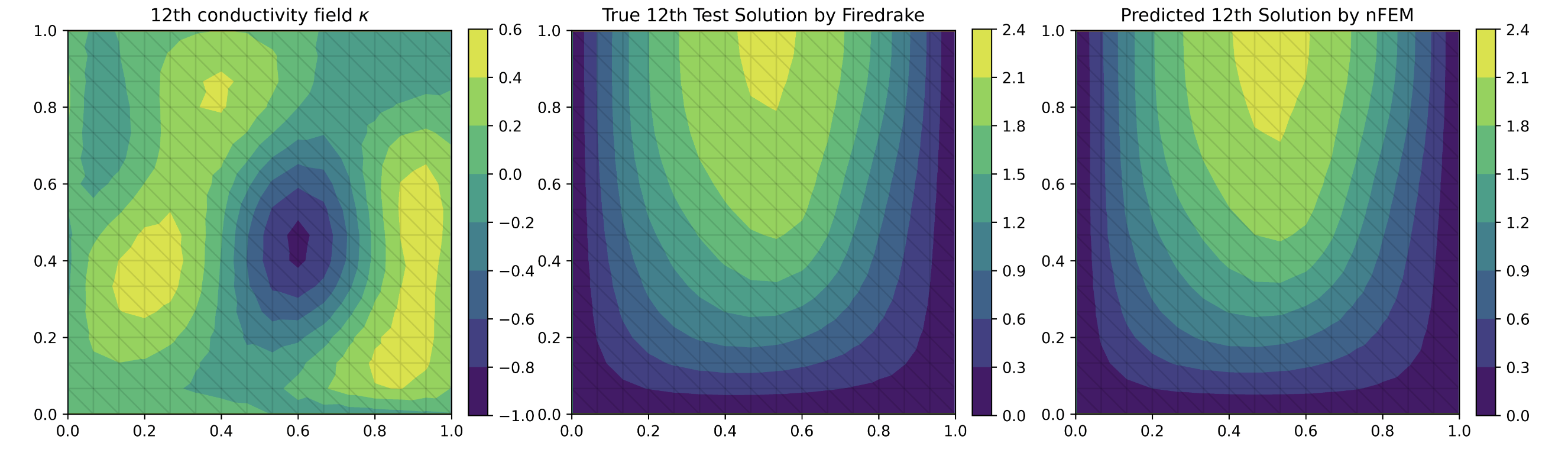
Figure 2: (Left) conductivity field, (Middle) True solution obtained by Firedrake software, (Right) Predicted solution obtained by TorchFire neural network