Major Activities

Neural networks are function approximators whose parameters exist in a very high dimensional space. Because of the layered and strongly inter-connected nature of neural networks, analysis can be difficult. To this end, active subspaces are leveraged as a computational tool for analysis of characteristics of the parameter space for a given neural network. We introduce the concept of a network condition number to measure how easily one can train a given neural network.

Significant Results

Last year we showed that that neural networks exhibit strong resistance to active subspace based dimension reduction techniques, indicating that all computation units are important.

The following figure illustrates the eigenvalues of the active subspace matrix for a network with 1 input neuron, 1 output neuron, and 5 hidden layers with 35 neurons per hidden layer, giving 5146 parameters total. The active subspace was estimated with ten thousand samples. The losses were calculated on a regression problem to regress a sin function.

The eigenvalues of the active subspace matrix for a network with 5146 parameters and 10000 active subspace samples.

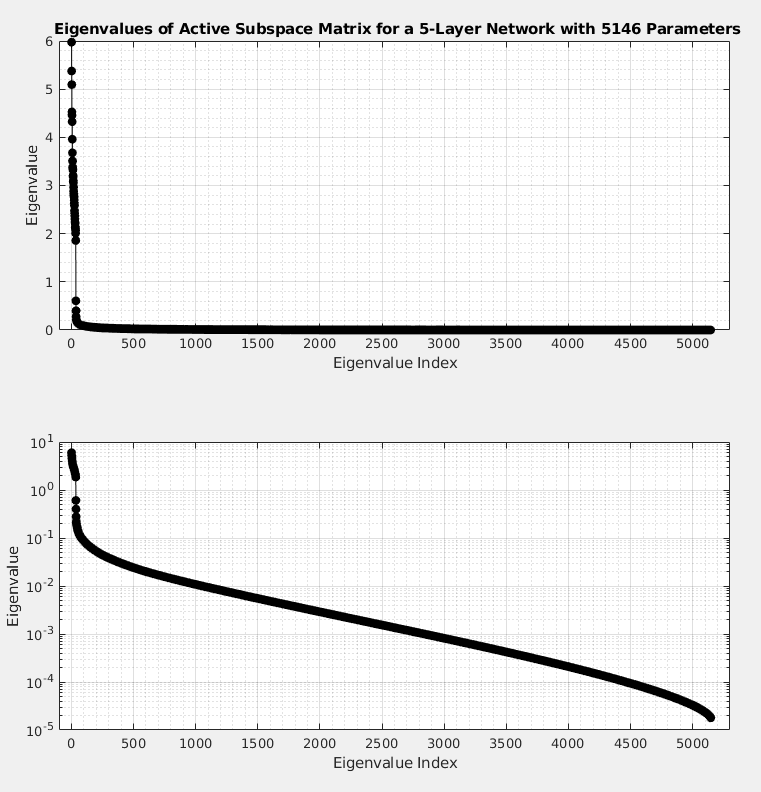
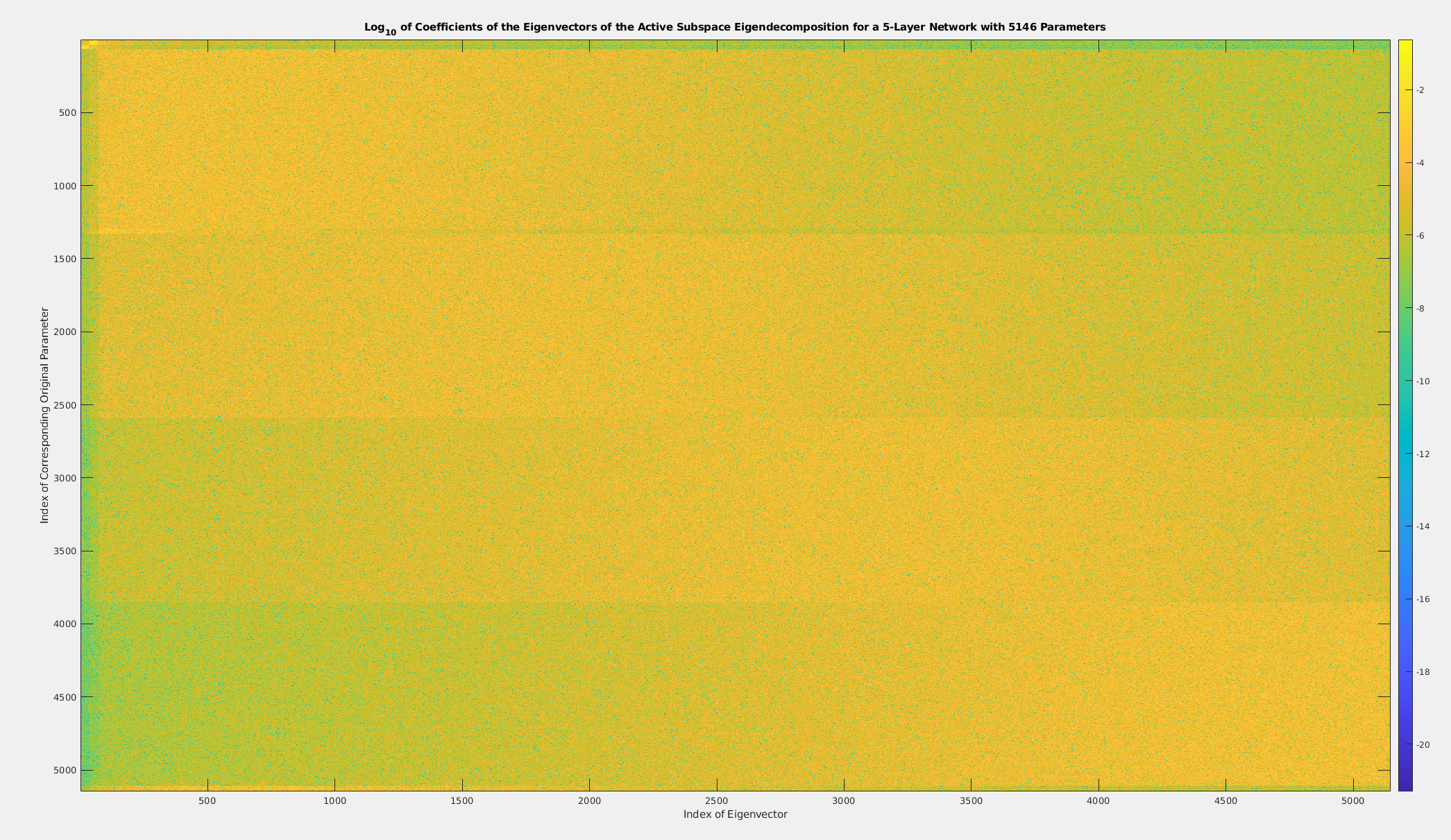
We have determined that some network parameters are more important than others, in the sense that the loss is more sensitive to them than others.

The eigenvectors of the active subspace matrix for a network with 5146 parameters and 10000 active subspace samples.

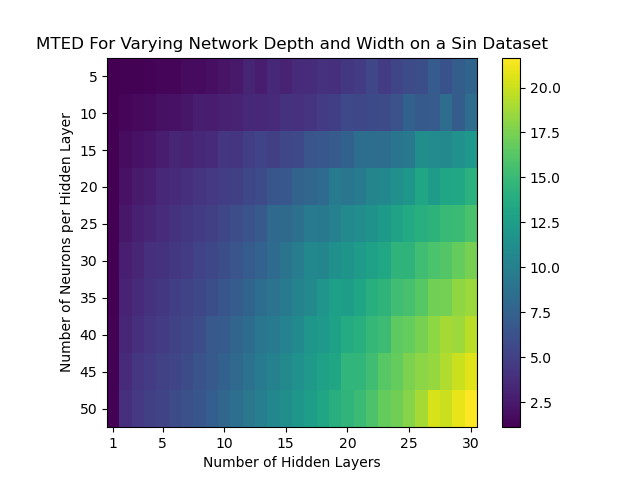
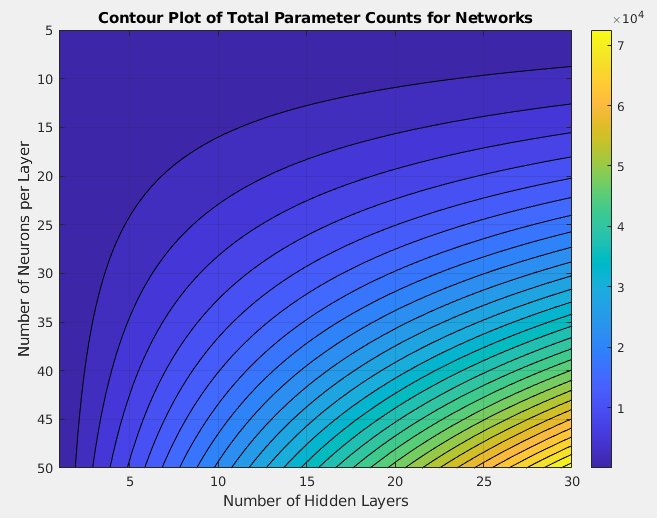
Further research has shown that we can create a network “condition number”. We see that for various network architectures, the network condition number behaves in a fashion that mimics the behavior of the total parameter count for a network.

The network condition number for dense fully connected networks evaluated on a sin regression.

A contour plot of the total number of parameters for dense fully connected networks.

Further analysis is underway to determine the active subspace behavior of model-constrained neural networks.