Randomized Approaches in Scientific Computing
Major Activities
Randomized Inverse Problems
Last year we developed asyptotic convergence analysis for linear inverse problems and numerically confirmed the convergence. This year, we extended this analysis to a broad class of nonlinear inverse and optimization problems. Additionally, we also proved a non-asymptotic convergence bound for subgaussian random variables. Under this unified framework, a variety of existing methods fall out as specializations. The beauty of such a framework, however, is that it can be used to uncover new randomization schemes that combine the best aspects of existing methods to accelerate both optimization and uncertainty quantification. Existing methods that are rediscovered include the randomized MAP method for posterior sampling, the randomized misfit approach (left sketching), and the ensemble Kalman filter.
Significant Results
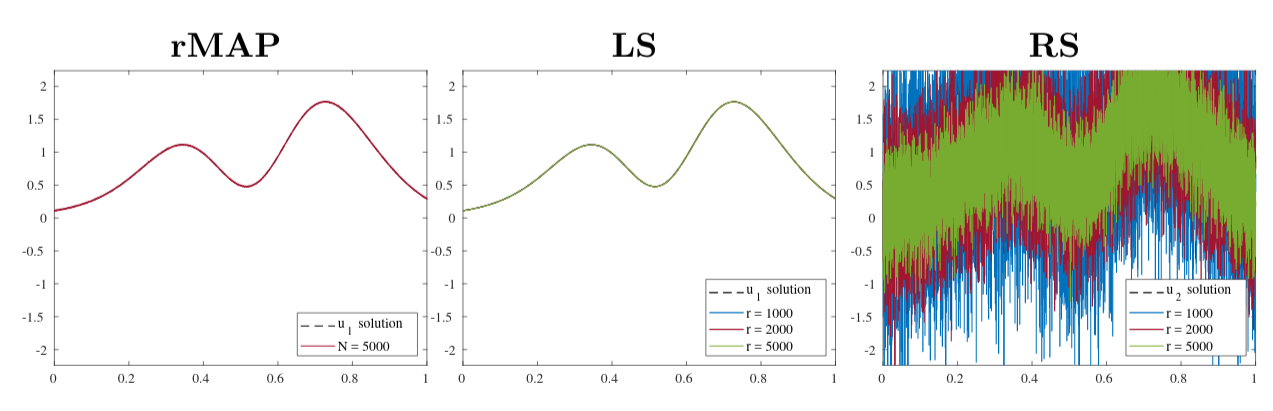
We analyze numerically the advantages of sketching the forward map
from the left compared to sketching from the right and compare results.
For the Shaw problem (P.C. Hansen, Regularization tools version 4.0),
we see that the randomized MAP (Wang, Bui-Thanh, Ghattas) and
left sketching approaches perform well with few samples while right sketching
performs poorly. We study this phenomenon from the viewpoint of regularization
and give recommendations on which regularization operators are well-suited for
use in a right sketching type method.