A Model-Constrained Discontinuous Galerkin Network (DGNet) for Compressible Euler Equations
Major Activities
This work has been started during the past year. We found that The Model-Constrained Discontinuous Galerkin Network (\(\texttt{DGNet}\)) emerges as a pioneering framework designed to address the pressing need for real-time, accurate solutions to large-scale dynamical systems governed by compressible Euler equations, a cornerstone of computational fluid dynamics (CFD) with applications spanning aerospace engineering, weather prediction, and hypersonic flow analysis. Traditional high-order numerical methods, such as the Discontinuous Galerkin (DG) approach, excel in capturing wave propagation and discontinuities like shocks but are hindered by significant computational burdens, including stability constraints from explicit time integration and the expense of implicit solvers or over-integration techniques for nonlinear problems. Meanwhile, machine learning approaches, such as Physics-Informed Neural Networks (PINNs), offer computational speed but falter in generalizing to unseen scenarios and handling solution discontinuities without retraining, limiting their practical utility in dynamic, real-world contexts like Digital Twins. \(\texttt{DGNet}\) bridges these gaps by integrating the strengths of DG methods with graph neural networks (GNNs) in a hybrid, model-constrained framework. Building on our prior mcTangent approach, \(\texttt{DGNet}\) learns the spatial discretization of DG while leveraging time integration schemes for temporal evolution, ensuring both computational efficiency and fidelity to physical laws. This approach introduces a suite of innovative strategies—time-invariance, physics enforcement, data randomization, input normalization, and high-order convergence preservation—enabling \(\texttt{DGNet}\) to generalize across diverse initial conditions, geometries, and meshes, even for out-of-distribution (OOD) scenarios, while maintaining stability and accuracy in capturing complex shock structures.
Specific Objectives
\(\texttt{DGNet}\) offers: (i) time integration schemes capturing temporal correlation, leveraging neural network speed for computation reduction; (ii) model-constrained approach ensuring learned tangent slope satisfies governing equations; (iii) graph neural network architecture with edges as Riemann solver surrogates and nodes as volume integration correction surrogates, enabling discontinuity capture, aliasing error reduction, and mesh discretization generalizability; (iv) input normalization for generalization across initial conditions, geometries, meshes, boundary conditions, and solution orders; (v) data randomization promoting agreement with true numerical models up to second-order derivatives, ensuring stability, prediction capacity, and enhanced generalization via data generation during training. It approximates the dynamical system \(\frac{\partial \boldsymbol{u}}{\partial t} + \mathcal{F}(\boldsymbol{u}) = 0\) with neural network \(\Psi_\texttt{DGNet}\), optimizing:
\[\begin{aligned} \mathcal{L} = & \sum_{i=2}^{n_{\mathrm{t}}} \left( \left| \overline{\boldsymbol{u}}^{i,1} - \tilde{\boldsymbol{u}}^{i,1} \right|{L^2(\Omega)}^2 + \left| \overline{\boldsymbol{u}}^{i,2} - \tilde{\boldsymbol{u}}^{i,2} \right|{L^2(\Omega)}^2 \right) \\ & + \sum_{i=2}^{n_{\mathrm{t}}} \left( \left| \boldsymbol{u}^{i,1} - \tilde{\boldsymbol{u}}^{i,1} \right|{L^2(\Omega)}^2 + \left| \boldsymbol{u}^{i,2} - \tilde{\boldsymbol{u}}^{i,2} \right|{L^2(\Omega)}^2 \right) \end{aligned}\]where:
\[\begin{aligned} \boldsymbol{u}^{i,1} &= S\left(\boldsymbol{u}^{i} + \Delta t \mathcal{F}(\boldsymbol{u}^{i})\right), & \boldsymbol{u}^{i,2} &= S\left(\frac{1}{2}\left(\boldsymbol{u}^{i,1} + \boldsymbol{u}^{i} + \Delta t \mathcal{F}(\boldsymbol{u}^{i,1})\right)\right), \\ \tilde{\boldsymbol{u}}^{i,1} &= S\left(\boldsymbol{v}^{i} + \Delta t \Psi_\texttt{DGNet}(\boldsymbol{v}^{i})\right), & \tilde{\boldsymbol{u}}^{i,2} &= S\left(\frac{1}{2}\left(\tilde{\boldsymbol{u}}^{i,1} + \boldsymbol{v}^{i} + \Delta t \Psi_\texttt{DGNet}(\tilde{\boldsymbol{u}}^{i,1})\right)\right), \\ \overline{\boldsymbol{u}}^{i,1} &= S\left(\boldsymbol{v}^{i} + \Delta t \Psi_\texttt{DGNet}(\boldsymbol{v}^{i})\right), & \overline{\boldsymbol{u}}^{i,2} &= S\left(\frac{1}{2}\left(\overline{\boldsymbol{u}}^{i,1} + \boldsymbol{v}^{i} + \Delta t \Psi_\texttt{DGNet}(\overline{\boldsymbol{u}}^{i,1})\right)\right), \end{aligned}\]with \(\boldsymbol{v}^{i} = \boldsymbol{u}^{i} + \boldsymbol{\epsilon}$, $\boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{\text{diag}}((\boldsymbol{u}^{i})^2))\), \(S\) as the slope limiter, and \(\Delta t\) as the time step. Uses second-order strong stability-preserving Runge-Kutta for high-order Discontinuous Galerkin convergence; any explicit time integration scheme applies. \(\texttt{DGNet}\) trains once, deploys for diverse mesh discretizations, reducing computational overhead while handling discontinuities effectively.
Significant Results
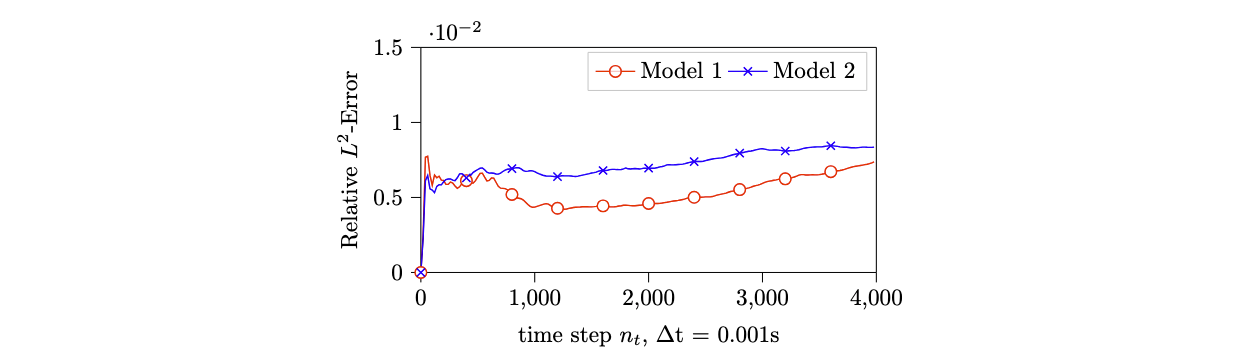
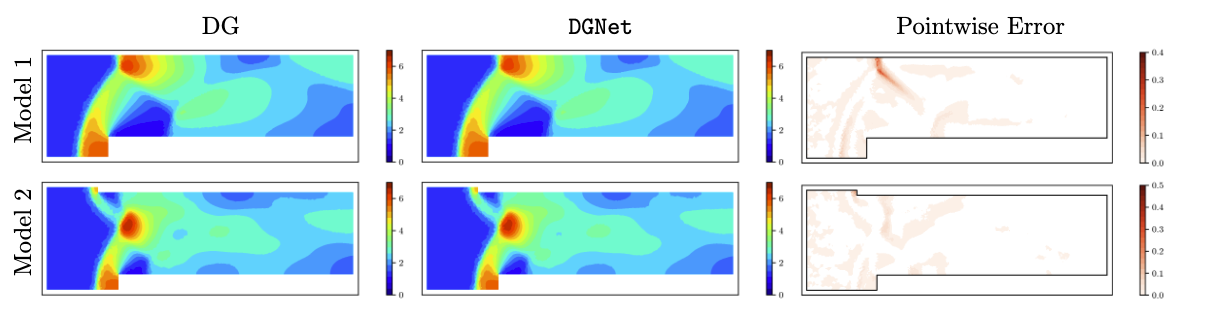
An example of \(\texttt{DGNet}\) applied to compressible Euler equations in a Forward Facing Step problem is shown in Figure 1 and Figure 2. \(\texttt{DGNet}\) is trained with data generated from Model 1 within the time interval \([0,1]\)s. Subsequently, the trained networks are used to predict the density field for both Model 1 (same geometry) and Model 2 (different geometry). The results demonstrate very low relative error at all time steps, as shown in Figure 1. Concurrently, \(\texttt{DGNet}\) solutions at \(T = 4\)s exhibit excellent agreement with the numerical DG solutions, as shown in Figure 2, while delivering a \(5\times\) faster solver.
More animations can be found at Animations for DGNet
More detail about this work can be found at Van Nguyen, H., Chen, J. U., & Bui-Thanh, T. (2025). A model-constrained discontinuous Galerkin Network (DGNet) for compressible Euler equations with out-of-distribution generalization. Computer Methods in Applied Mechanics and Engineering, 440, 117912.