Last year, we explored methods to reduce the computational cost of numerically integrating stiff ODEs and PDEs. The main speed bottlenecks for integration of stiff systems are small timestep requirements for numerical solver and often the necessity of an implicit, rather than explicit, integration scheme. To resolve the expensive time requirements of integration, we designed a machine learning, surrogate model architecture which can solve stiff systems without step size requirements and can be utilized to predict all time steps in the system in parallel. The approach has the capability to approximate stiff systems to a high degree of accuracy in a fraction of the time of the original solver.

Major Findings

We evaluated our method using three stiff systems of ODEs and two stiff PDEs: the Robertson ODE, Collisional Radiative Charge States and Energy States ODEs, and the Allen-Cahn and Cahn-Hilliard PDEs. All of the dynamical systems considered are highly-stiff and some even have multiscale solutions, making these problems extremely challenging for traditional machine learning integration schemes, such as Neural ODE. On each test problem, our approach outperforms two state-of-the-art machine learning techniques, Neural ODE and DeepONet.

Significant Results

The following first table shows the prediction error, in the relative L2 norm, for each machine learning approach, on each problem. It is clear that our proposed approach outperforms all other approaches in terms of accuracy. In the table, OOM indicates that a model could not be trained on our hardware because the memory costs were too high. The second table shows the speedup achieved by our method in comparison to a traditional numerical solver for each given problem. Row one shows the total time taken by the numerical solver and our proposed approach to compute the solutions for \(1000\) initial conditions, while row two shows the same for the surrogate approach. We see that our approach achieves O(1)-O(3) speedup on all problems, in terms of wall clock computation time. Finally, the figure shows a side-by-side comparison between a solution to the Cahn-Hilliard PDE and the machine learning approximation of the solution, as well as giving the point-wise absolute error between the two methods. The initial condition was not seen by the network in training. The proposed model has very close agreement to the numerical solution, with a maximum absolute error on the order of \(10^{-2}\). The bottom right plot of the figure shows the average relative L2 norm error over time across 200 test initial conditions.

image image

Cahn Hilliard PDE Results

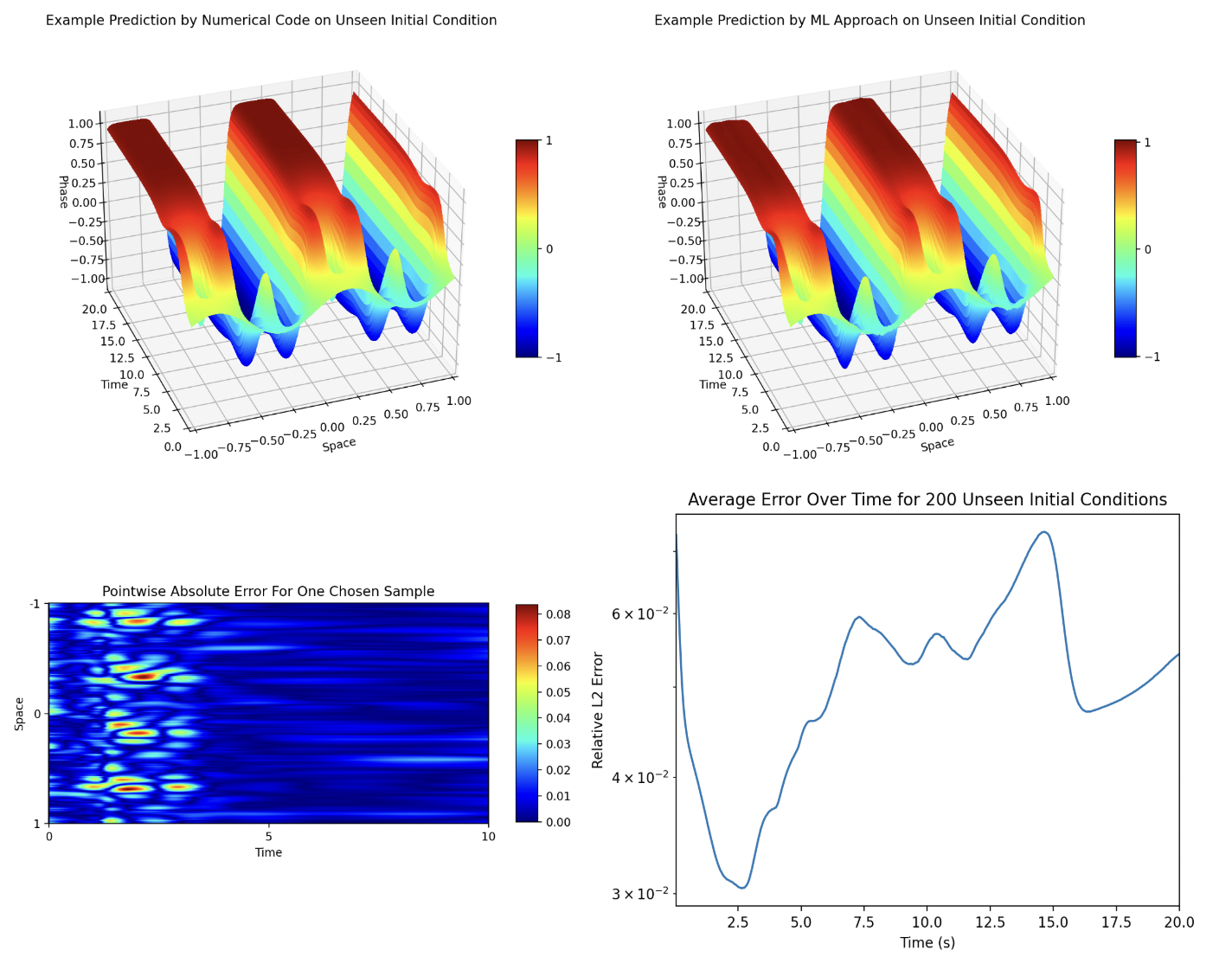
image

More detail about this work can be found at https://arxiv.org/abs/2105.12033.