Randomized Approaches in Scientific Computing

Major Activities

Randomized Inverse Problems

We have developed a unified framework under which we can study and understand randomized approaches to solving inverse problems. We show that this various randomized approach to solving inverse problems can be viewed as special cases of this more general framework. In particular, we prove asymptotic convergence results for a broad class of randomizations using stochastic optimization theory. Our unified framework not only recovers many existing methods (including gradient descent, coordinate descent, Karzmarz method, etc) but also discovers new ones.

Significant Results

Randomized Inverse Problems

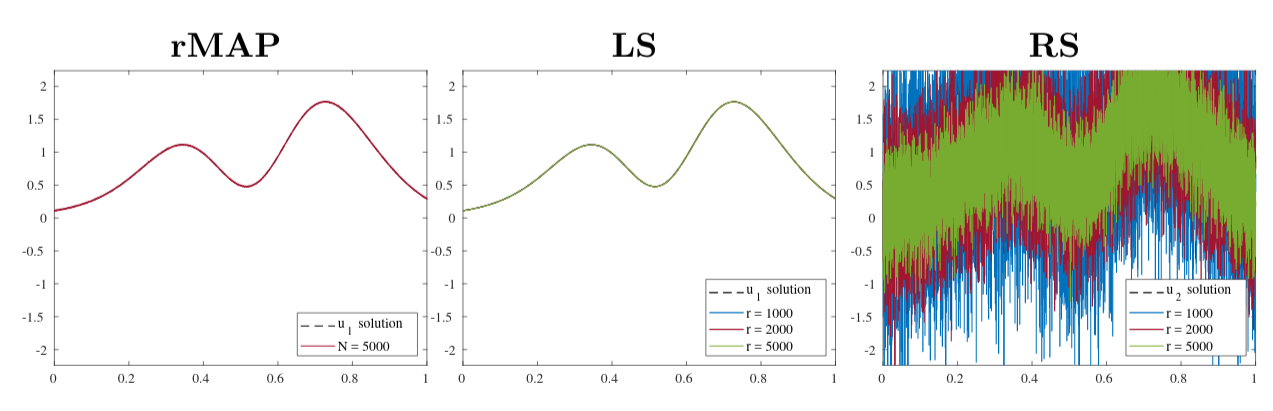
We analyze numerically the advantages of sketching the forward map from the left compared to sketching from the right and compare results. For the Shaw problem (P.C. Hansen, Regularization tools version 4.0), we see that the randomized MAP (Wang, Bui-Thanh, Ghattas) and left sketching approaches perform well with few samples while right sketching performs poorly. We study this phenomenon from the viewpoint of regularization.

Ensemble Kalman Inversion

Recently, the use of Ensemble Kalman filter as an inverse problem solver has received considerable interest where it is referred to as the Ensemble Kalman Inversion (EnKI). By revisiting the derivation of EnKI from a different perspective, we have developed a class of convergence improvement strategies leading to faster convergence to the true solution.

For the 1D Deconvolution problem, the rate of convergence using the developed strategy is demonstrated in Figure below. Vanilla EnKI refers to the traditional EnKI algorithm.

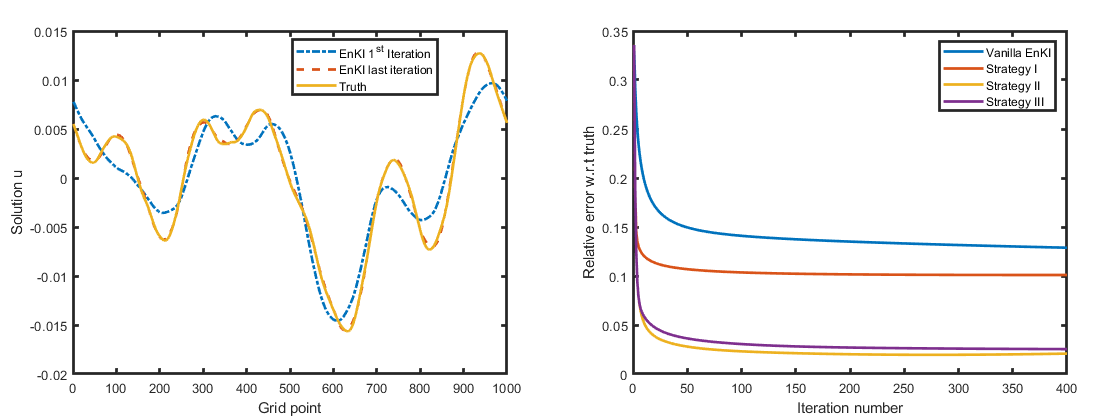
Fig 1: Reconstructed Solution corresponding to strategy III (Left); Convergence rate for different methods (Right)