Deep-learning enhanced model reduction method

Major Activities

This project focus on forecasting solution of time-dependent PDE’s using Neural Networks. The process is further enhanced by applying model reduction strategy. The idea is to approximate the PDE solution \(u(t,x)\) as a linear combination of basis functions:

\[u(t,x)=\sum_{j=1}^r U_j \alpha_j(t)\]

A neural network is then used to fit the time-dependent coefficients (\(\alpha_r(t):\) \(r\) dimensional output) at different time instants (\(1\) dimensional inputs). However, this approach can only predict solution within the training data set and fails at forecasting the solution accurately at a future time instant (i.e outside the training data set). In order to deal with this issue, we have developed a model-constrained approach to take the underlying mathematical model into account.

For model order reduction, we consider either the Proper orthogonal decomposition (POD) or Dynamic mode decomposition (DMD).

Significant Results

For demonstration, we consider the linear advection equation driven by an external force. A time-varying boundary condition is adopted and only the first two dominant modes are considered for approximating the solution. The forecasted solution when one uses POD is shown below. It is clear that one can forecast the solution accurately at a future time instant by encoding the mathematical models into the learning process.

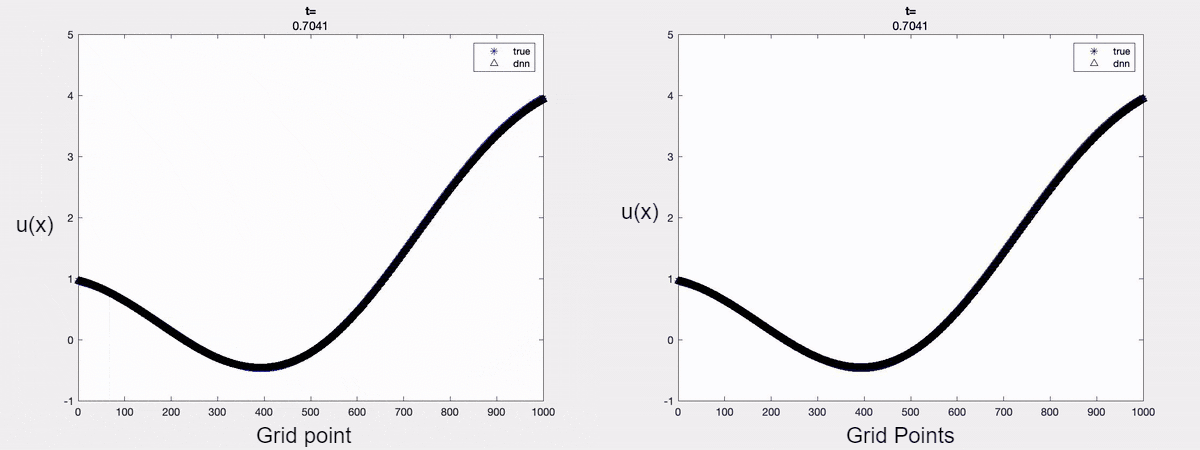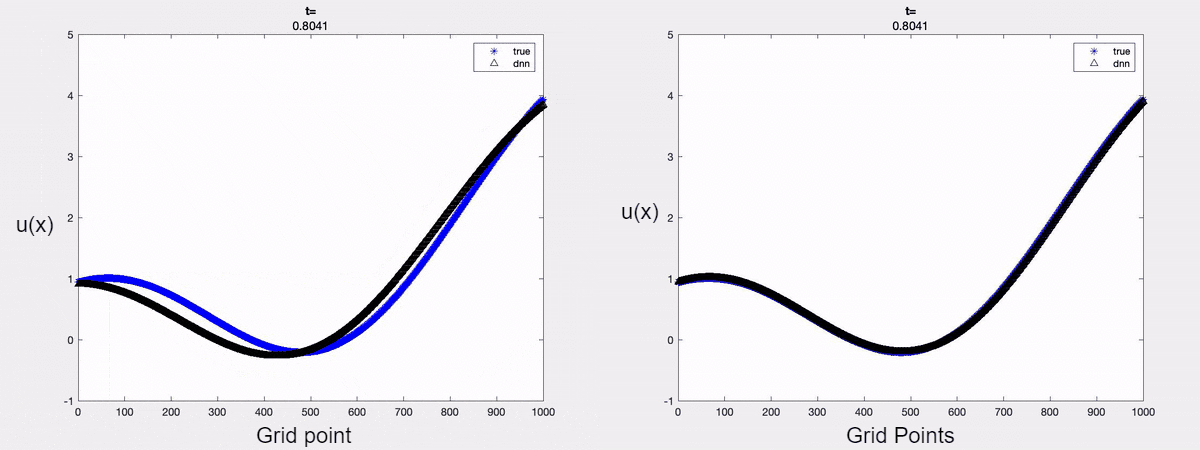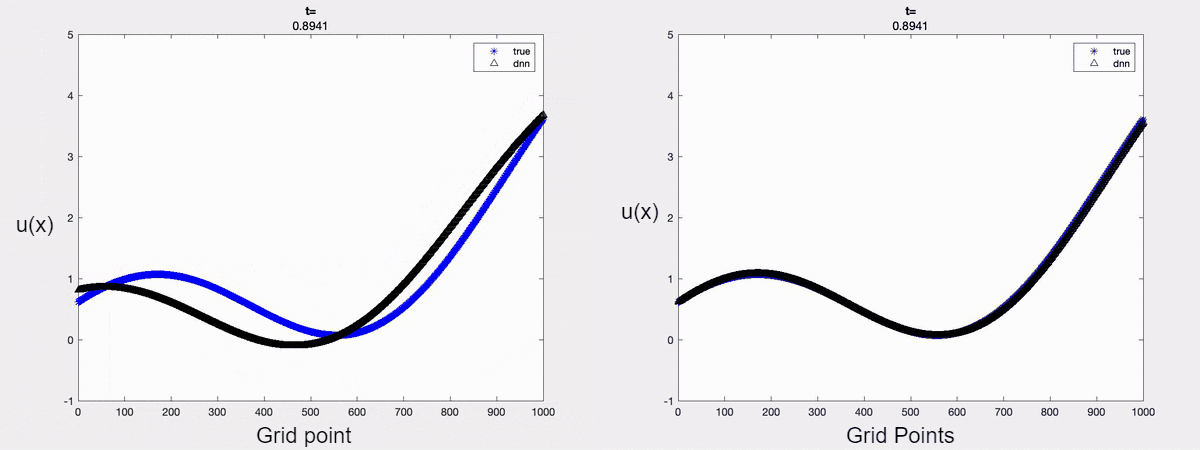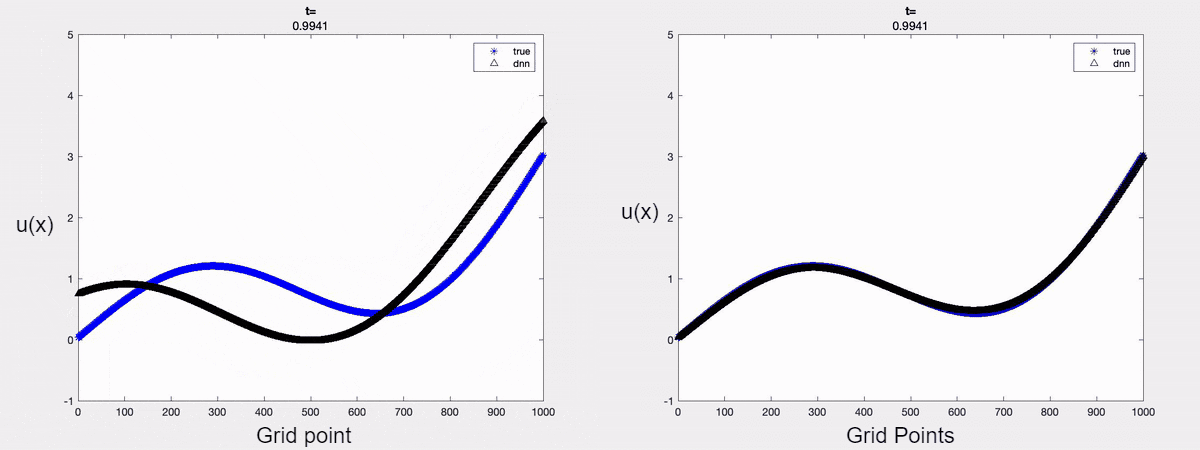
 Fig 1 (left to right): a) Forecasted solution without the Physics constraint;
 b) Forecasted solution with the Physics constraint.