Toward a Rigorous and Reliable Scientific Deep Learning Framework for Forward, Inverse, and UQ Problems
 Figure 1: Predictions with error and uncertainty during the training process to solve a Poisson inverse problem.
Figure 1: Predictions with error and uncertainty during the training process to solve a Poisson inverse problem.
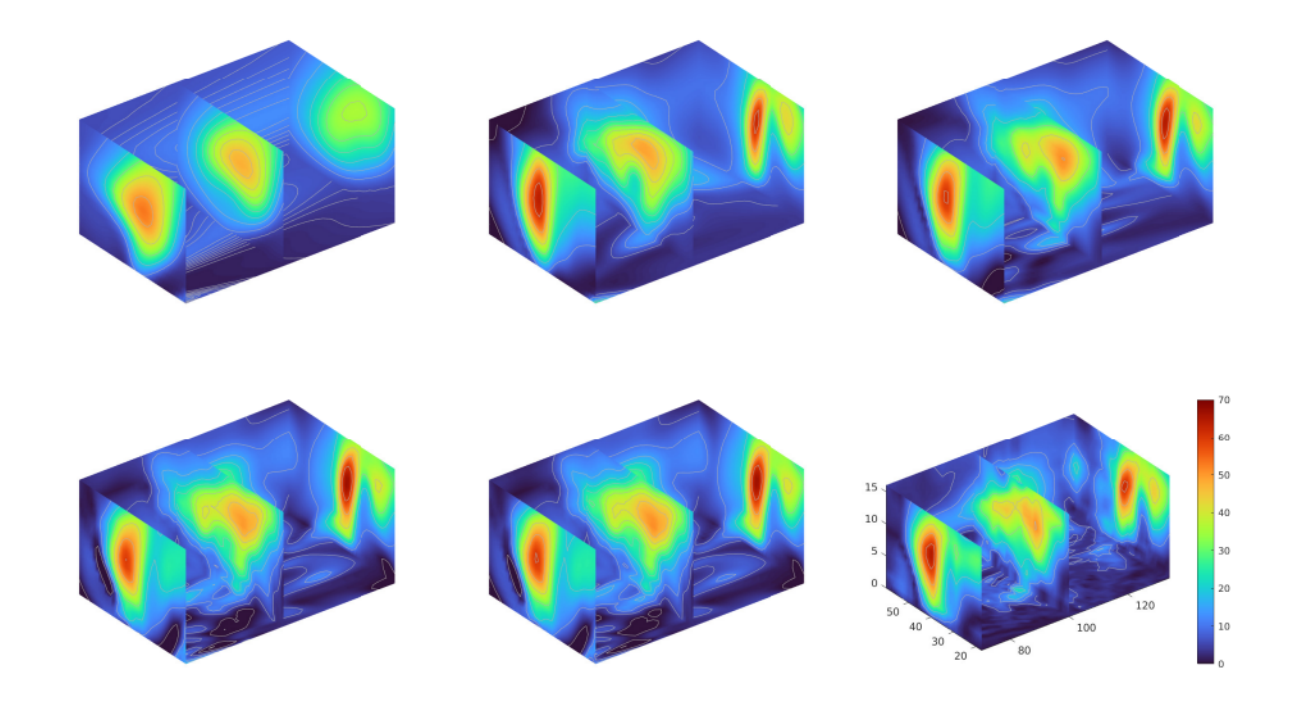 Figure 2: Evolution of solution (3D air current profile) upon adding new hidden layers in architecture adaptation.
Figure 2: Evolution of solution (3D air current profile) upon adding new hidden layers in architecture adaptation.
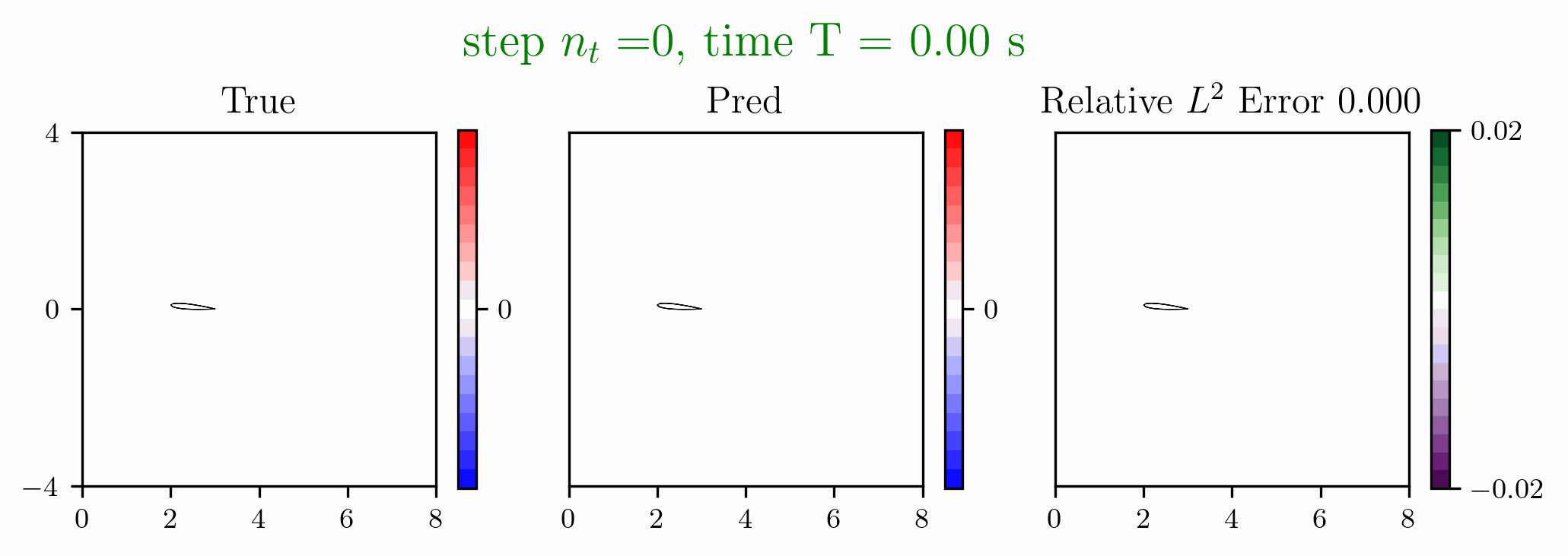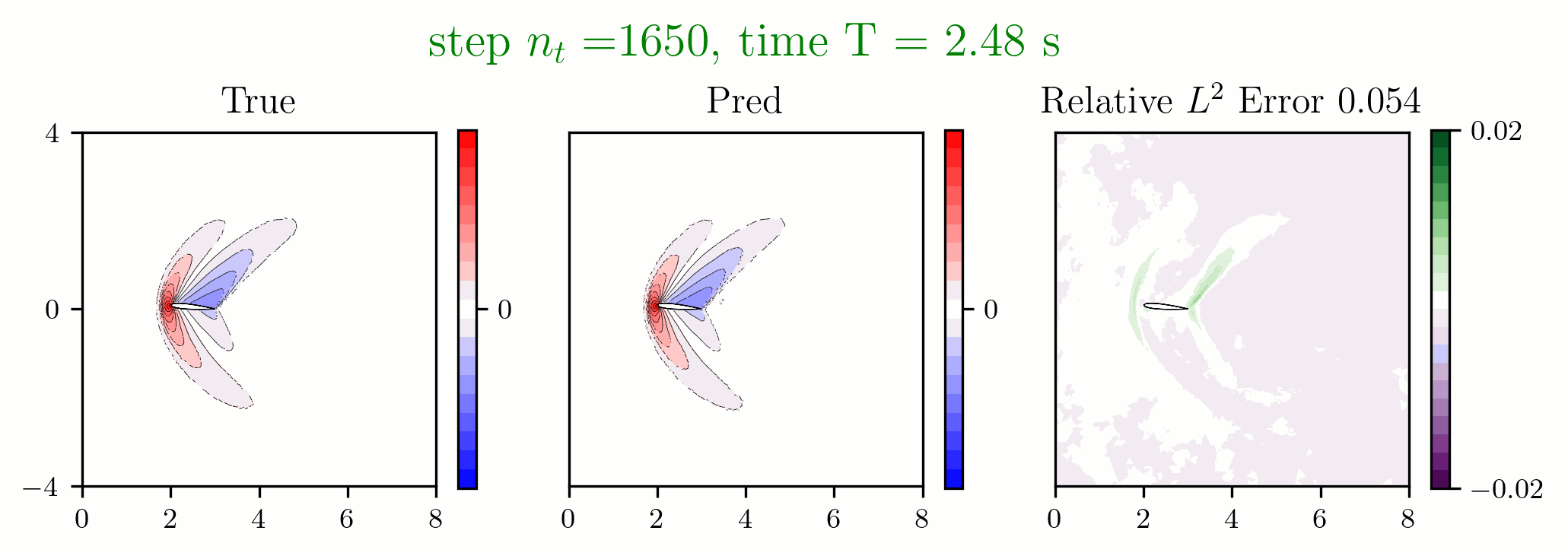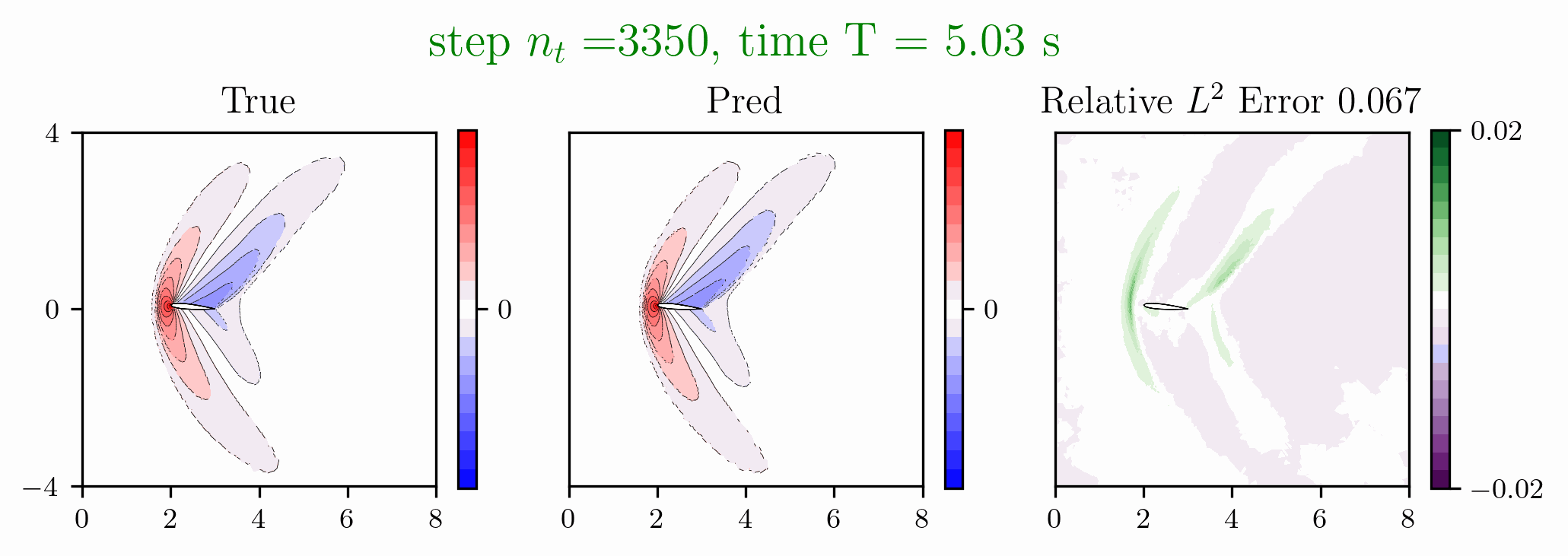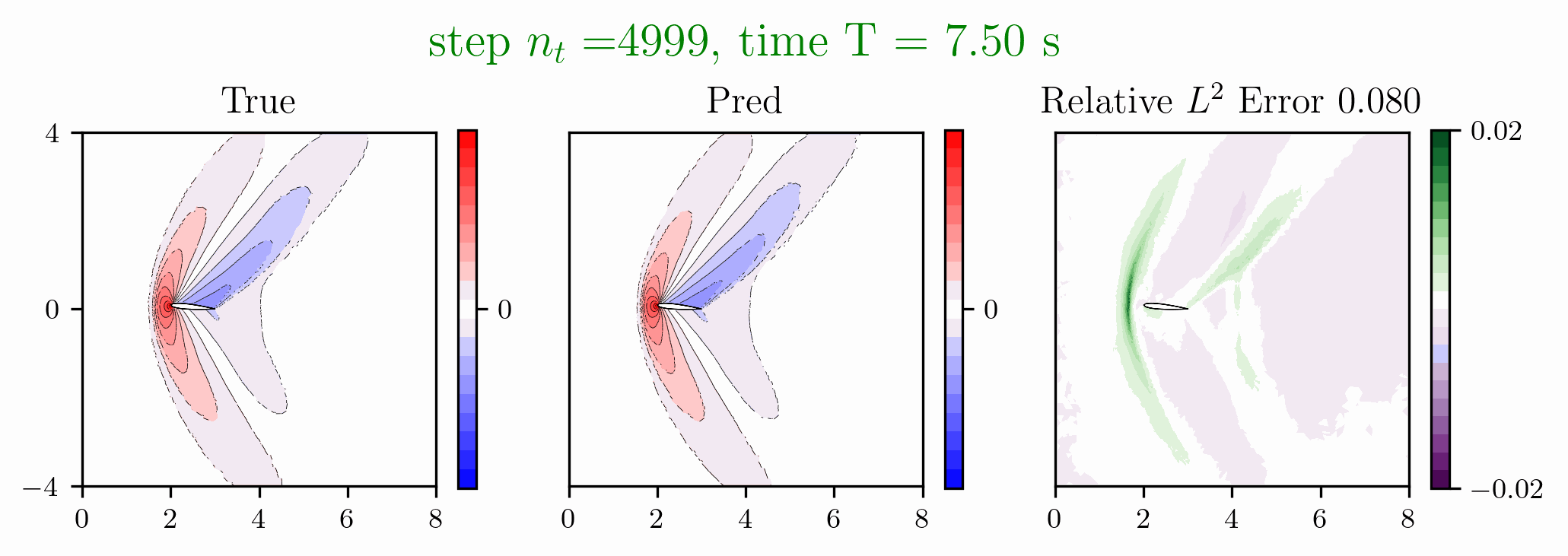 Figure 3: Predictions made on an airfoil after solving the Euler equations.
Figure 3: Predictions made on an airfoil after solving the Euler equations.
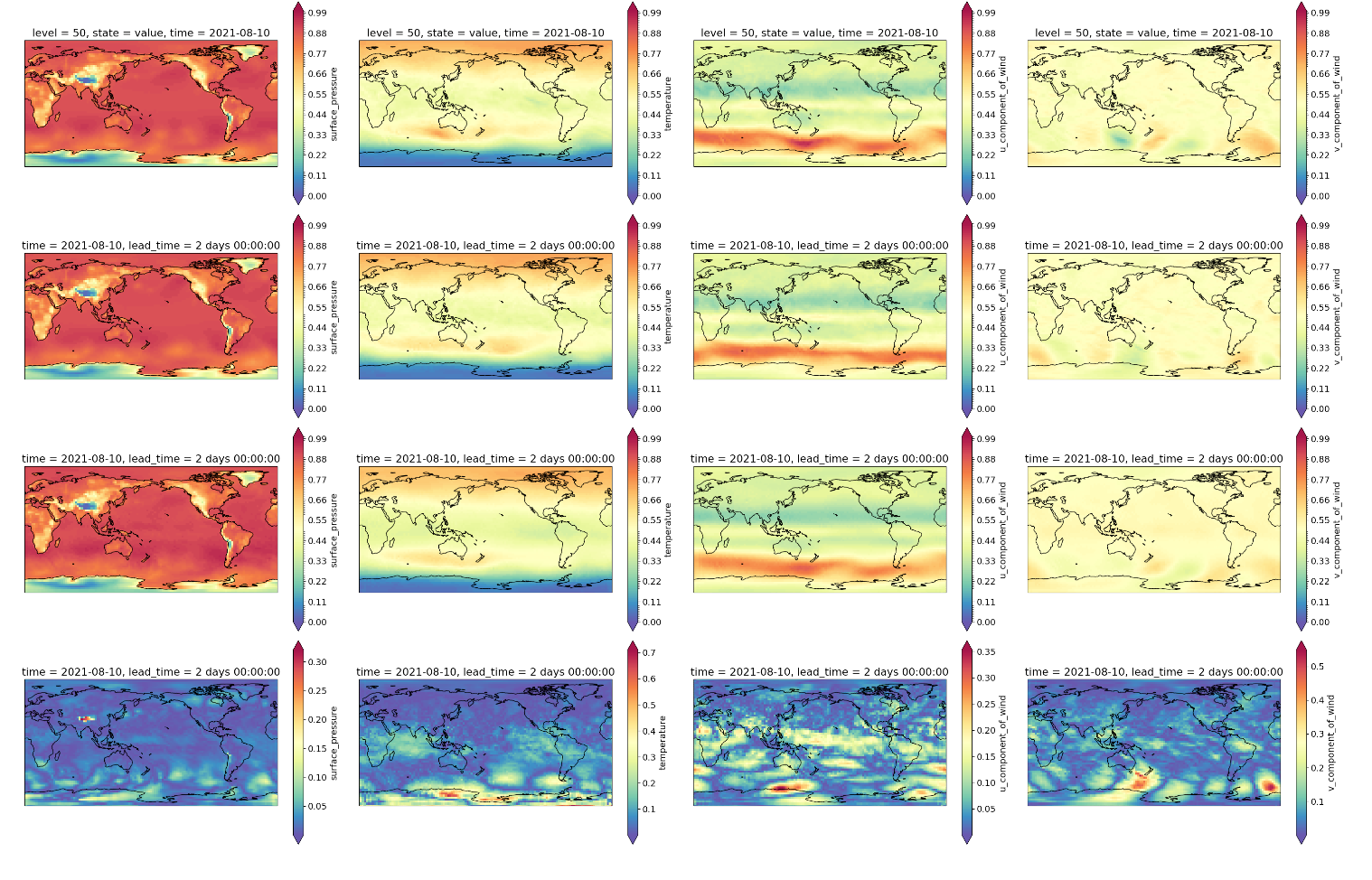 Figure 4: Snapshots of weather forecasts via physics-constrained deep learning.
Figure 4: Snapshots of weather forecasts via physics-constrained deep learning.
Table of Contents
Aims
Aim 1: Develop rigorous and adaptive architecture design for deep learning
One of the key challenges in adapting deep learning methods to science and engineering problems is how to determine the architecture of deep learning for the problem under consideration. Leveraging well-developed applied math techniques to develop rigorous approaches for architecture design.
Aim 2: Develop model-constrained deep learning methods for forward and inverse simulations
Many data-driven science and engineering problems governed by physic laws, e.g. governing equations have limited experimental or observational data. In this case, pure data-driven deep learning approaches are prone to over-fitting and thus not capable of respecting the mathematical models. Capitalizing on our decade of experience on large-scale forward simulations, we shall develop model-constrained deep neural network methods to encode the underlying mathematical models in order to obtain fast and accurate forward and inverse solutions.
Aim 3: Develop model-constrained uncertainty quantification for deep learning
Most, if not all, deep learning approaches do not take into account the variability in the data and the uncertainty in training, and neither do they provide uncertainty associated with deep learning predictions. Leveraging our expertise in Bayesian inversion and uncertainty quantification (UQ), we shall develop a model-constrained Bayesian approach to quantify the uncertainty in deep learning solutions.
Aim 4: Develop efficient model updating methods for deep learning
Deep learning models, like other surrogate modeling techniques, may not suitably generalize depending on the training datasets used. As new information readily becomes available, it is desirable to incorporate this knowledge into a previously developed model. It is particularly desirable to do this in an efficient manner by utilizing prior information, such as the domain-specific physics or mathematical properties of the system being modeled. From our extensive experience in modeling and simulation, we develop new methods incorporating such information to update models efficiently.
Projects
- Active Learning with Neural Architecture Adaptation
- Discontinuous Galerkin-Graph Neural Network
- Uncertainty Quantification for Deep Learning
- Physics-Constrained Deep Learning Models for Weather Forecasting
Undergraduate research
- B-Functions and Quadrature-Based Neural Networks
- Memory-based Medium-range Weather Forecasting
- Learning Navier Stokes in the Frequency Domain
Publications
[1] Lee, Jeonghun J, Tan Bui-Thanh, Umberto Villa, and Omar Ghattas, Forward and inverse modeling of fault transmissibility in subsurface flows, Computers and Mathematics with Applications, Volume 128, 15 December 2022, 354-367.
[2] S Muralikrishnan, S Shannon, Tan Bui-Thanh, A multilevel block preconditioner for the HDG trace system applied to incompressible resistive MHD, Computers Methods in Applied Mechanics and Engineering, Volume 404, 1 February 2023, 11575.
[3] Hai V. Nguyen, Tan Bui-Thanh, A Model-Constrained Tangent Slope Learning Approach for Dynamical Systems, International Journal of Computational Fluid Dynamics, Volume 36, Issue 7.
[4] Ella Steins, Tan Bui-Thanh, Michael Herty, Siegfried Müller, Probabilistic constrained Bayesian inversion for transpiration cooling, Numerical Methods in Fluids, Volume 94, Issue 12, 2020-2039.