Activation Functions, Universality, and \(\mathcal B_\theta\) Functions

Activation functions are a critical component of Deep Neural Networks. Their non-linear structure and universal properties enable the network to model a wide variety of problems. Given their frequent occurence, many have proposed the question: which activation function is best? To answer that question, we studied the universal property of traditional activation functions and constructed a Neural Network architecture that utilizes quadrature in order to aid the resulting approximation.

Many traditional activation functions have proven to be universal via the construction of Neural Network Approximate Identity (denoted nAI or \(\mathcal B_\theta\)), a family of bell-shaped curves which are a combination of a given activation function. With quadrature, these nAI can approximate any continuous function with accuracy increasing with respect to the number of quadrature points. By implementing a Neural Network that utilizes quadrature, we hope to give a fair comparison between the effectiveness of different activation functions across a variety of problems.

Results

Our initial experiments were conducted with the purpose of evaluating this quadrature approximation and its convergence to some random function. The figures below depict how the quadrature increases in accuracy as the number of quadrature points goes from 10 to 20.

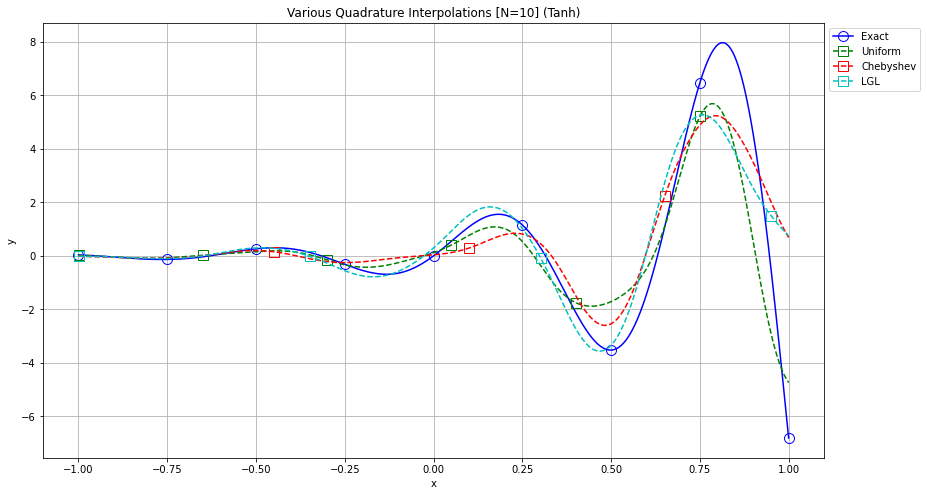
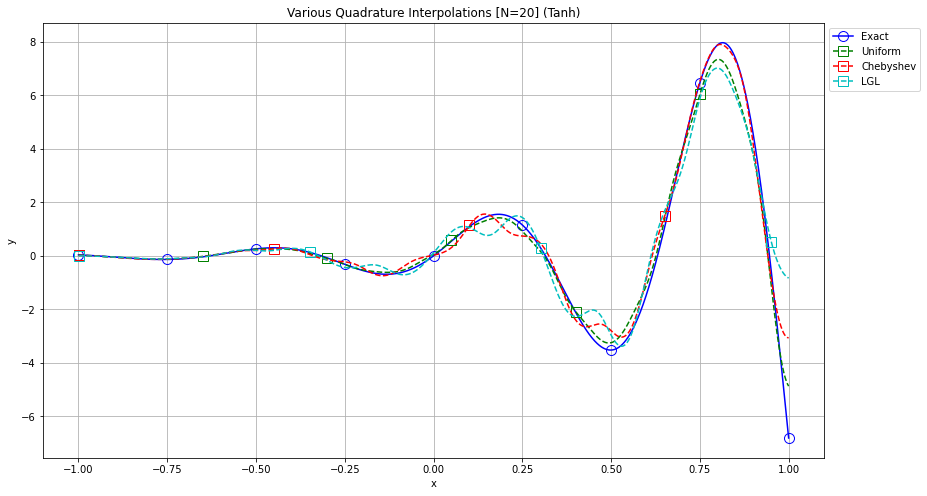
Quadrature Approximation (N=10) Quadrature Approximation (N=20)

By implementing a Neural Network that mimics the quadrature approximations above, we were able to better approximate the function with few points, as given in the next figure.

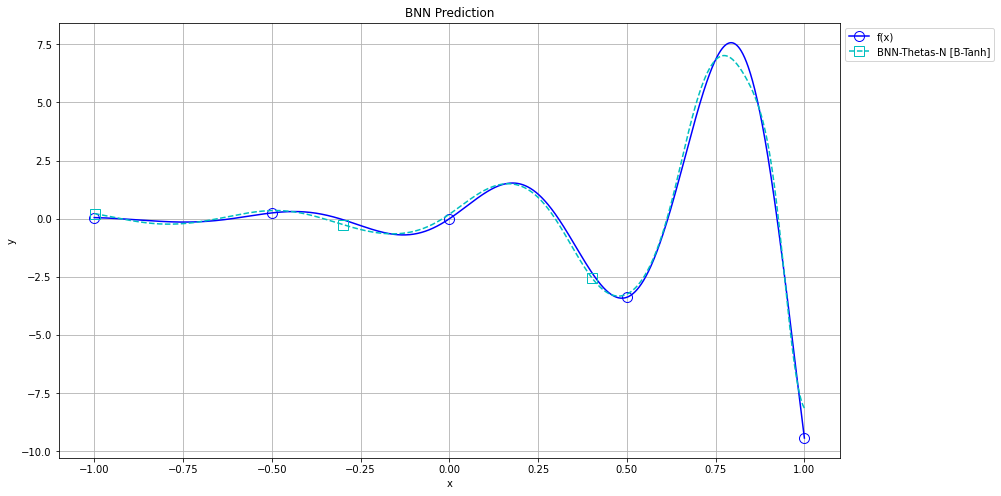
QBNN Approximation (N=10)

With a successful implementation of QBNN, current steps involve using QBNN and other standard Neural Networks to compare several traditional activation functions using nAI.