Introduction about project

Expanding on the concepts from our earlier work mcTangent, we introduce DGGNN, an end-to-end learning framework that combines a model-constrained Discontinuous Galerkin method with graph neural networks, inspired by tangent slope learning. This approach aims to create a surrogate model approximating the tangent slope of conservation law equation systems. The surrogate model integrates graph neural network architecture with the high-order DG method in a hybrid fashion. A dual mesh mechanism is formed by the graph neural network and the nodal data used in the DG method, with DG nodal values serving as graph neural network node attributes. The graph neural network edges, analogous to numerical fluxes in the DG method, model interactions between point pairs on shared edges of adjacent elements. By synthesizing the mcTangent approach, the DG method, and graph neural networks, DGGNN offers several advantages over existing methods. First, it learns the underlying tangent slope of conservation law equations, allowing the trained neural networks to be used with both explicit and implicit time integration schemes. Second, during training, it ensures the surrogate model satisfies discretized governing equations, maintaining adherence to conservation laws. Third, it employs a data randomization technique, promoting similarity between derivatives of the learned tangent slope and the numerical discretized solver, thus bounding prediction error and enhancing stability for long-term predictions beyond the training horizon. Fourth, neural network inputs are normalized to a unified range of \([-1,1]\) across all data sets, enhancing generalizability for solving unseen scenarios or different problems on complex geometries. Fifth, it preserves the high-order convergence rate of the DG approach, maintaining numerical accuracy.

Results

We applied the proposed approach to 1D shock-type problems, including the Burger equation and the Sod tube problem, as well as 2D and 3D linear problems, yielding promising outcomes. Additionally, the approach has been extended to tackle more complex scenarios, encompassing 1D and 2D Euler equations, and 3D Navier-Stokes equations. The proposed method demonstrates remarkable generalizability, allowing for training neural networks with specific data sets that can then be applied to solve significantly different contexts, including initial conditions, geometry, and Mach number.

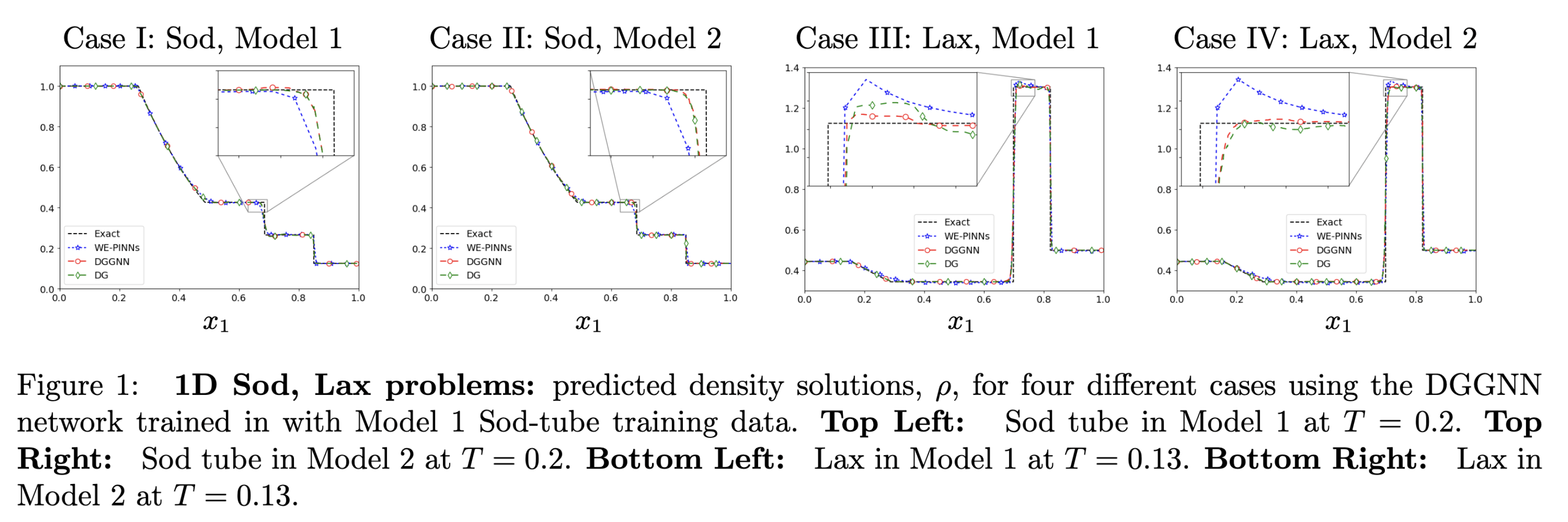
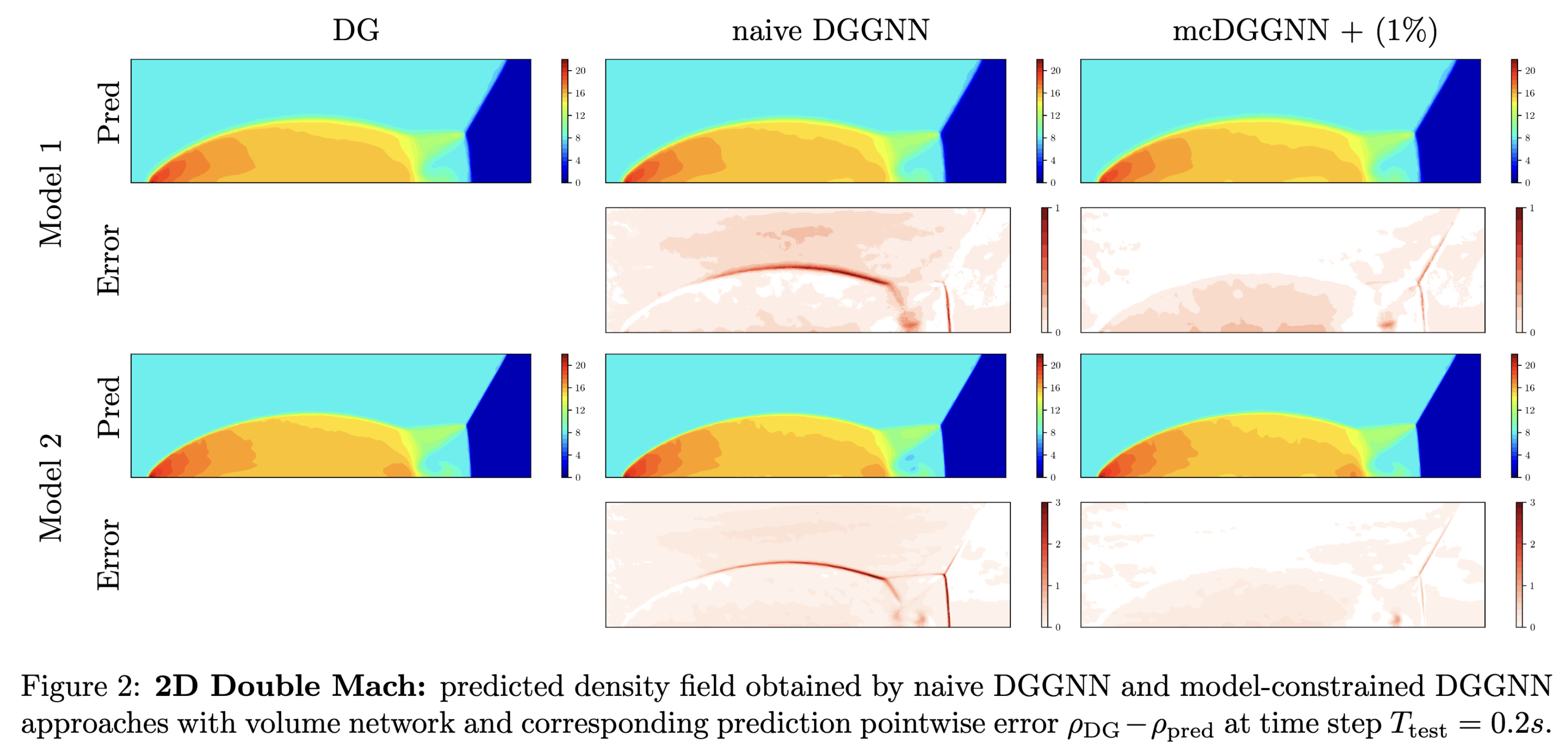
The results for the 1D Sod-tube and Lax problems are illustrated in Figure 1. The neural network, trained using Case I in Model 1 data, was subsequently employed to solve the Sod tube and Lax problems in Model 2. The findings indicate that the neural network can accurately predict solutions for three additional cases with substantially different initial conditions and mesh discretizations. Figure 2 presents the results for the Double Mach problem (2D Euler equations). In this instance, the neural network was trained using Model 1 data (comprising 60,192 triangular elements) and then utilized to solve Model 2 (consisting of 240,768 triangular elements). The results demonstrate the neural network’s capability to predict solutions for the Double Mach problem across significantly different mesh discretizations.

Fig1

Fig2