Physics-Constrained Deep Learning Models for Weather Forecasting
Motivation
Weather forecasting has been traditionally conducted via numerical weather prediction (NWP). In this approach, the equations of motion governing the fluid dynamics of the atmosphere on Earth are approximated via several numerical schemes and then solved. These forecasts, which are limited by the physical assumptions of the equations used in the models, have been corrected via data assimilation strategies to improve accuracy. However, this entire process is expensive due to the need of demanding computational resources for numerically solving the discretized equations and the need of large memory capacity to store the data. Our aim is to obtain accurate medium-range weather forecasts (on the order of three to seven days) via machine learning for reducing these storage and computational costs. Instead of numerically solving fluid dynamics models, such as the Navier-Stokes equations via computational fluid dynamics simulation methods, a faster approach for forecasting is to develop a surrogate model. This development requires suitable parametric models to capture complex physical effects, such as advection and turbulence, and extensive data that capture these effects. Deep neural networks are potentially suitable parametric models with their universal approximation properties. Sizeable datasets have been generated based on NWP and data assimilation methods, such as ERA5 reanalysis. Purely data-driven approaches based on deep learning and this reanalysis data have been previously developed for medium-range weather forecasting, particularly models such as GraphCast and Pangu-weather representing the state-of-the-art. The cost of training these surrogate models, however, can also be prohibitively expensive in terms of computing resources typically available only to large corporations. To address these challenges, we have been developing methods to incorporate physics knowledge into machine learning models to reduce computational costs where appropriate, and utilize the advantages of machine learning with data to compensate for the limitations of physical models in terms of accurate formulation and computational costs of simulations.
Results
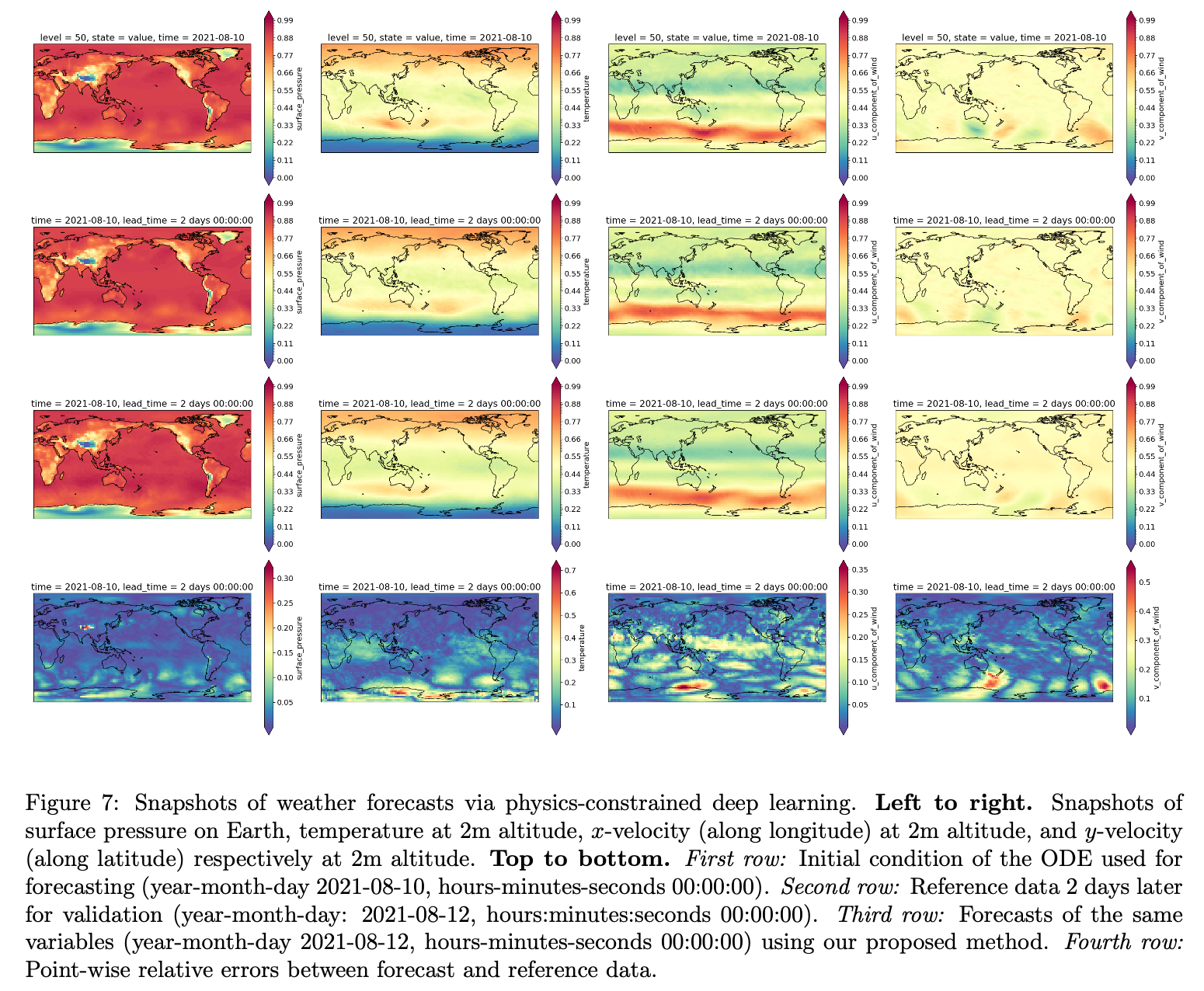
Our proposed approach is to utilize historical data with an appropriately developed reduced-order model to reduce the computational costs of weather forecasting with similar accuracy as NWP. Specifically, we propose a deep learning architecture in the form of an ordinary differential equation (ODE). In this approach, known physical symmetries (e.g., advection, diffusion, etc.) are enforced in the architecture for reducing computational costs and improving generalization capabilities. The unknown and expensive computations (e.g., turbulence structures, data assimilation corrections) are modeled as source terms whose mathematical relationships are determined from data and the physics constraints via deep learning. The model has been trained on ERA5 reanalysis data with one year of observations to minimize the forecasting error of the proposed model at six-hour intervals. In this process, desirable training time has been observed on low- and medium- resolution weather data using a single graphics processing unit on a modest computing cluster. A demonstration of the forecast using the method is shown below, which depicts the forecast two days later starting from 2021-08-10 at midnight. The advection effects, which are enforced in the model, are captured in the forecast as desired. The accuracy is expected to improve with including more training data, which is part of ongoing work.