Data-informed Regularization
Major Activities
Using experimental or measured data to infer a quantity of interest is the central task in solving inverse problems in the deterministic setting. Often the inverse of the parameter-to-observable map (PtO map) is ill-posed, resulting in difficulty estimating the underlying parameter or quantity of interest that generated the data. To overcome the ill-posedness of the inverse map, regularization techniques are often employed. Traditional regularization techniques such as Tikhonov and Total Variation (TV) regularize all parameter directions thus polluting those directions which are informed by the data. We have developed a novel regularization technique, which we call the Data-Informed approach (DI), that regularizes only the directions which are not informed by the data — that is, the directions which are dominated by noise. The method is developed in the deterministic setting and then extended to the statistical setting through derivation of the DI posterior distribution. This enables us to not only predict the underlying quantity of interest, but to characterize it’s uncertainty in a manner that is consistent with the data.
In the deterministic setting, the DI loss functional can be written as
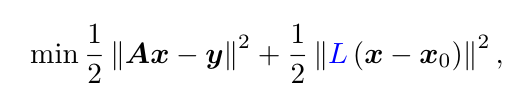
where
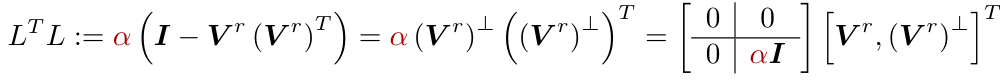
and V are the right singular vectors of A. Thus the DI method does not pollute the data-informed directions with unnecessary regularization. Additionally, we constructively derive the DI posterior distribution by writing the DI method in the statistical setting. We give numerical results comparing the DI method with the Truncated SVD method and Tikhonov regularization for image deblurring, image denoising, and x-ray tomography problems.
Significant Results
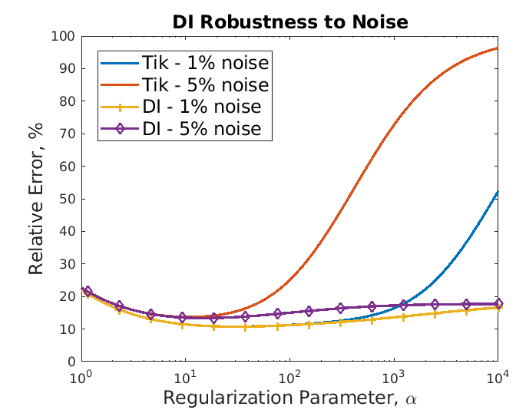
One compelling advantage of the DI method over other traditional regularization methods, expecially Tikhonov regularization, is that the DI method is robust with respect to choice of the regularization parameter. For the image deblurring problem and letting r=400, the following figure shows that the DI solution error remains low as the regularization parameter increases while Tikhonov regularization leads to large error with large regularization parameter.
Since the DI posterior knows which “directions” in which to be more confident in and which to be more uncertain in, we expect the DI posterior to be more informative about where uncertainty exists in the solution. We show numerically that this is the case and that, compared to Tikhonov regularization, the DI posterior is more conservative with its estimate of uncertainty. The figure below shows the pointwise variance from the solution to a deblurring problem with 100% and 10% of the data, 5% noise, and regularization parameter 1000. The Tikhonov posterior gives lower uncertainty than the DI posterior and, especially in the case of missing data, the DI posterior is more uncertain in the regions with missing data than the regions where we have data.

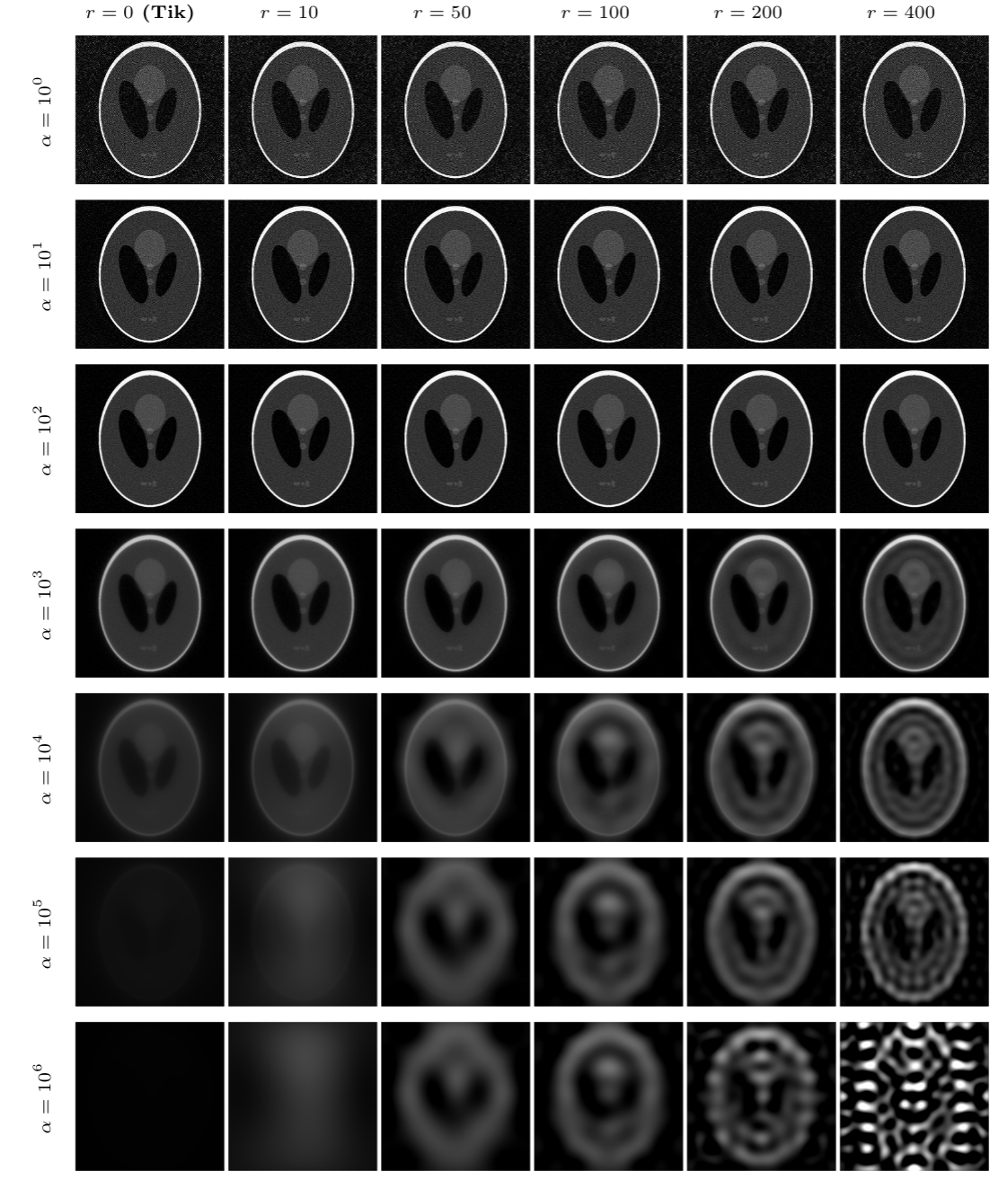
Below are reconstructions for the x-ray tomography reconstructions. The first column shows the Tikhonov solution and the other columns show the DI solution for various choices of r. Each row corresponds to a different value of the regularization parameter. The DI solution quality does not decay as quickly as the Tikhonov solution.
This work has been accepted for publishing in the Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging. A preprint version of this work can be downloaded from the Oden Institute for Computational Engineering and Sciences.