CAREER - Scalable Approaches for Large-Scale Data-driven Bayesian Inverse Problems in High Dimensional Parameter Spaces
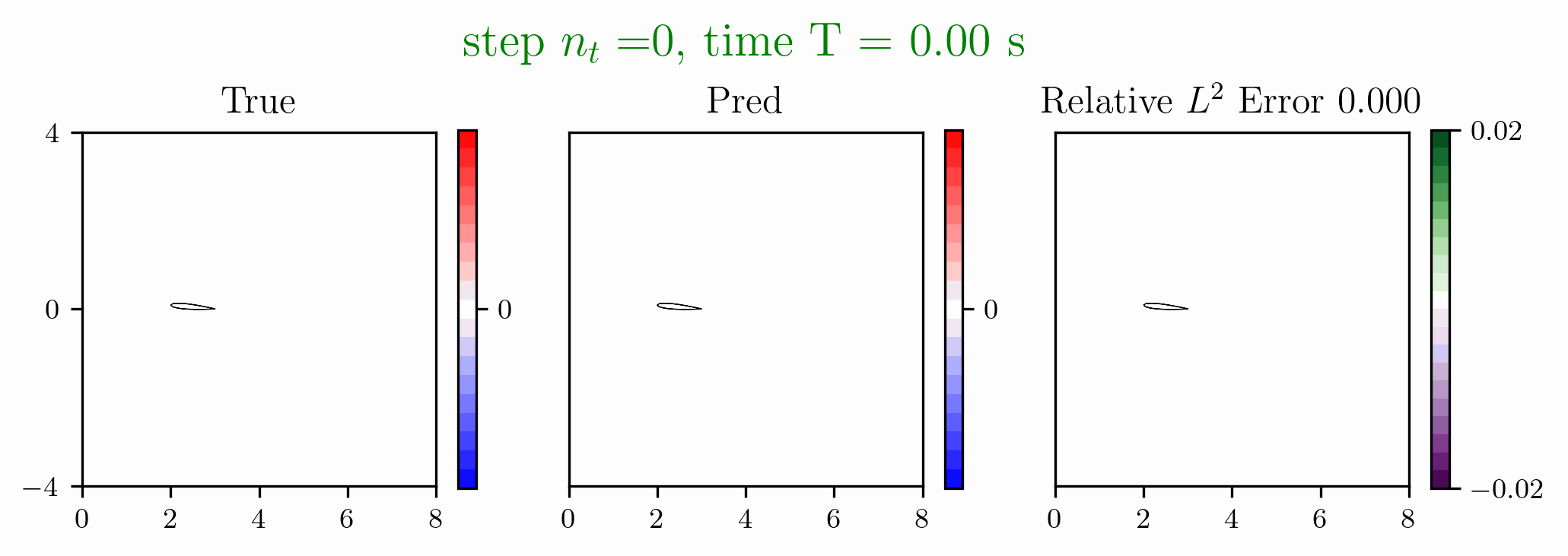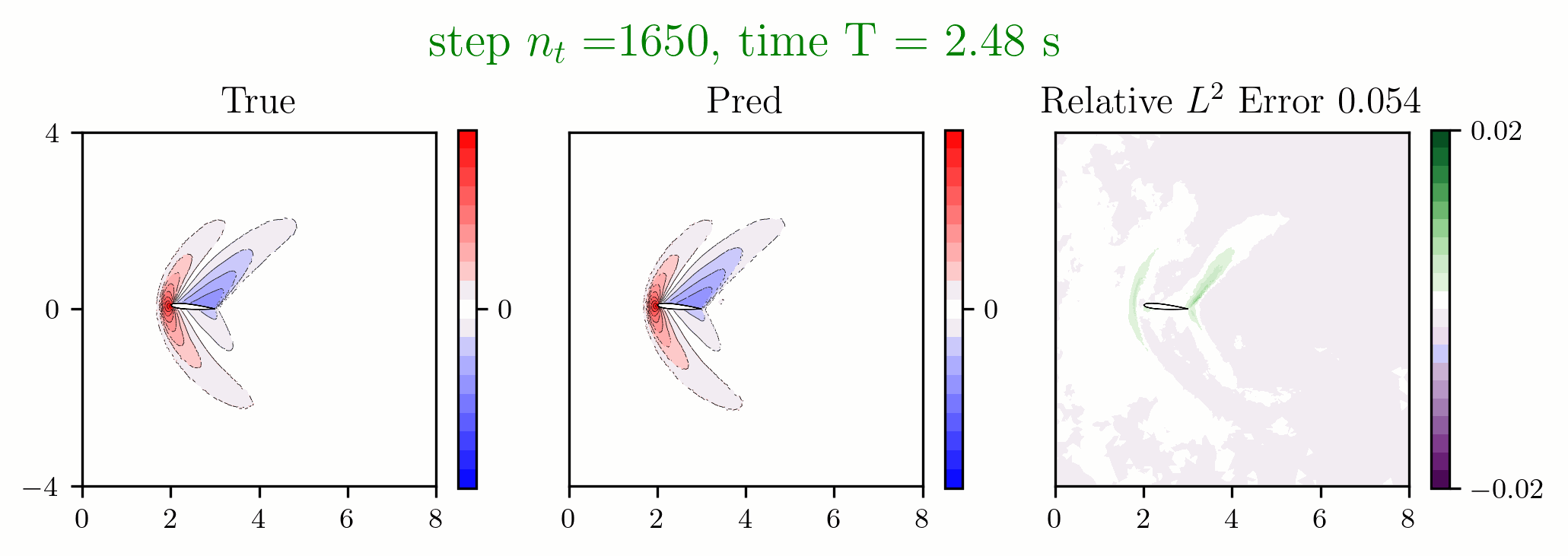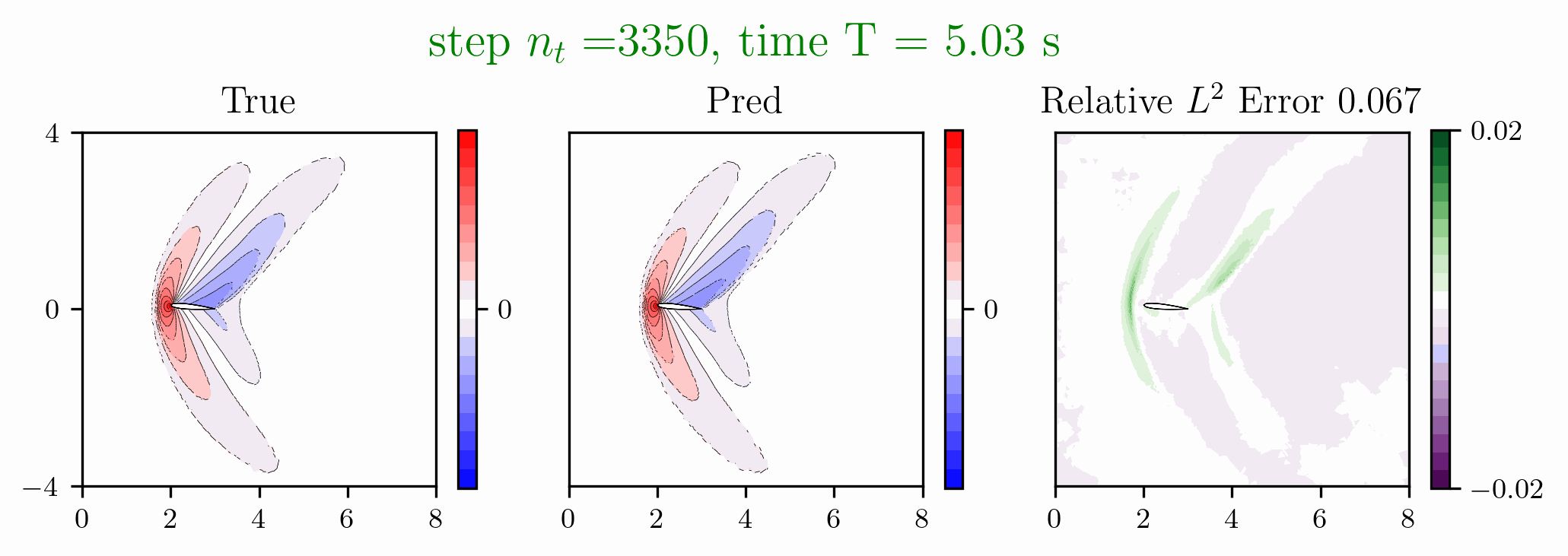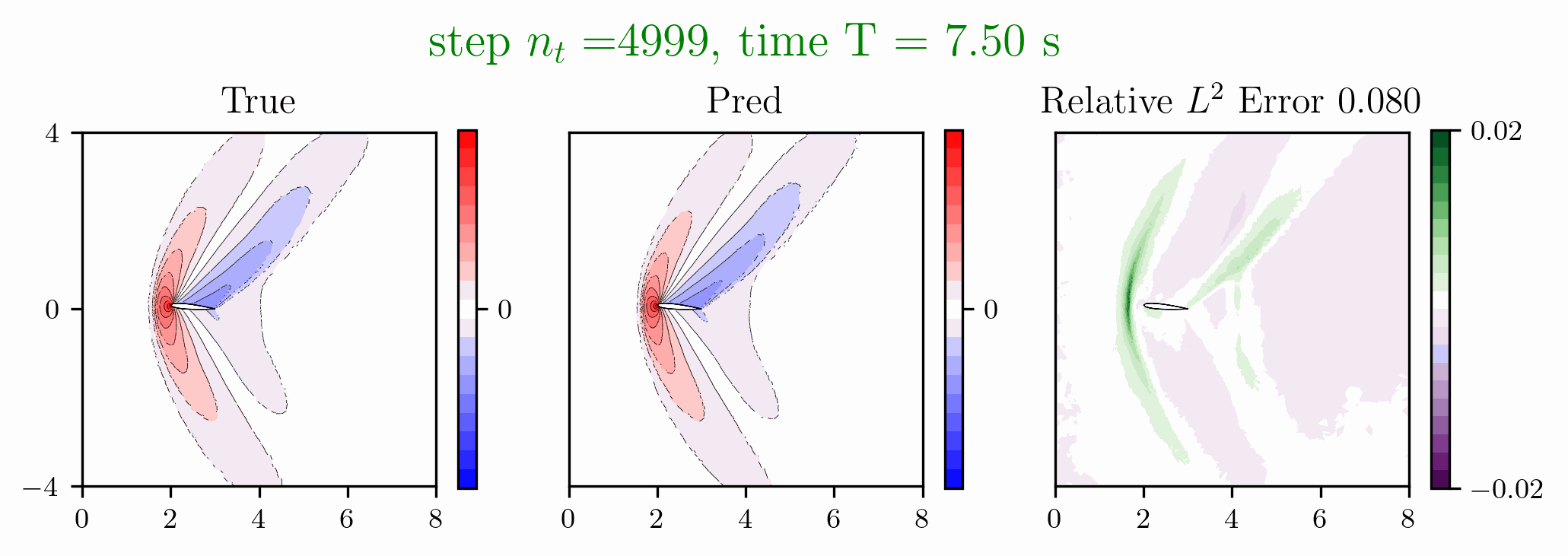 Figure 1: Predictions made on an airfoil after solving the Euler equations with DGGNN approach.
Figure 1: Predictions made on an airfoil after solving the Euler equations with DGGNN approach.
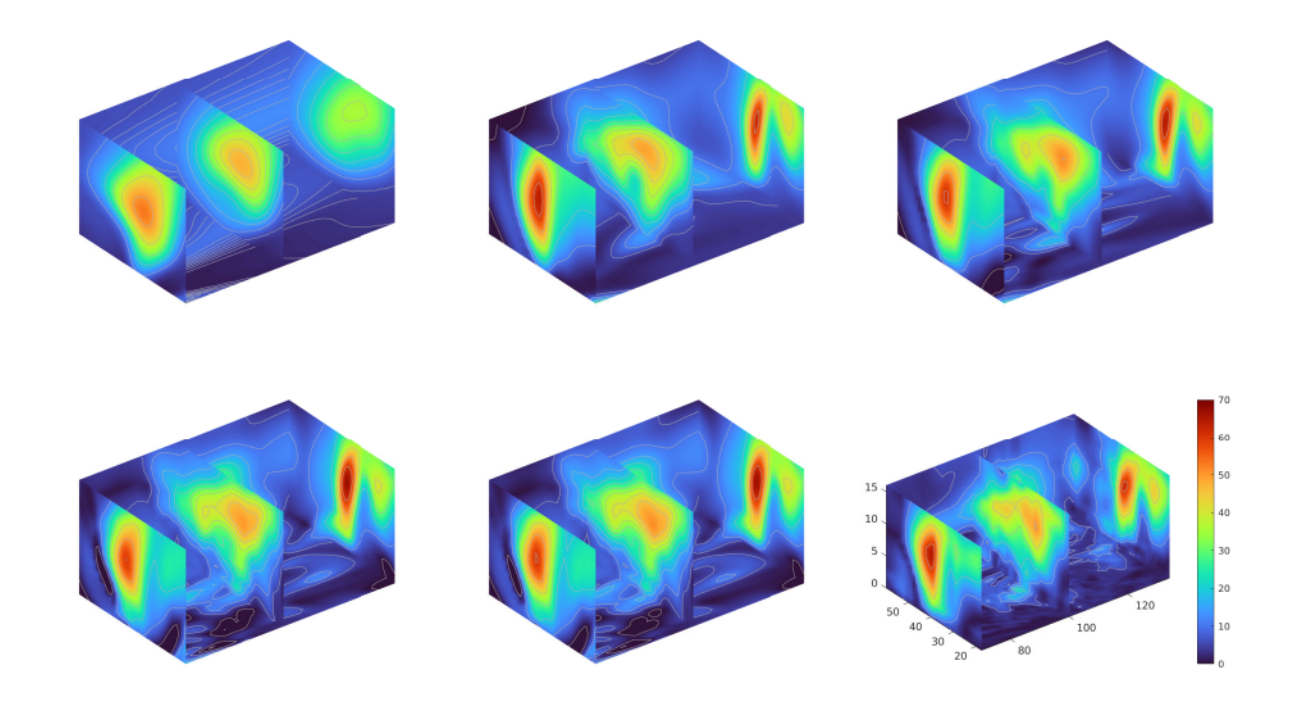 Figure 2: Evolution of solution (3D air current profile) upon adding new hidden layers in architecture adaptation.
Figure 2: Evolution of solution (3D air current profile) upon adding new hidden layers in architecture adaptation.
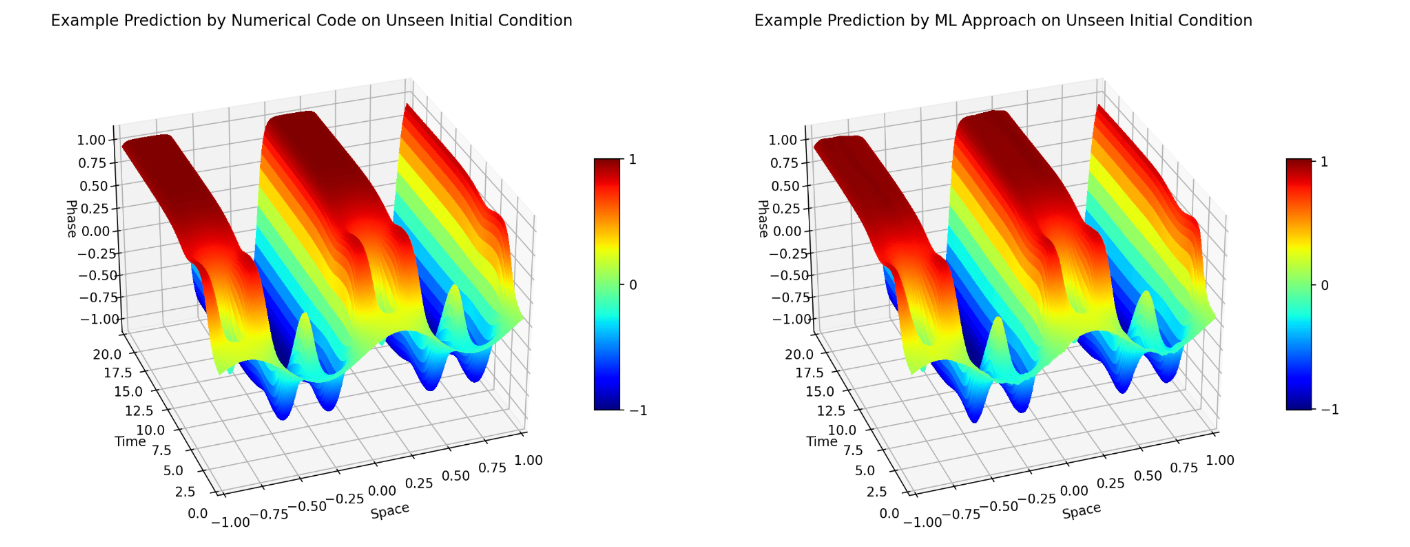 Figure 3: A high-dimensional latent space approach to predict the solutions of Cahn Hilliard PDE.
Figure 3: A high-dimensional latent space approach to predict the solutions of Cahn Hilliard PDE.
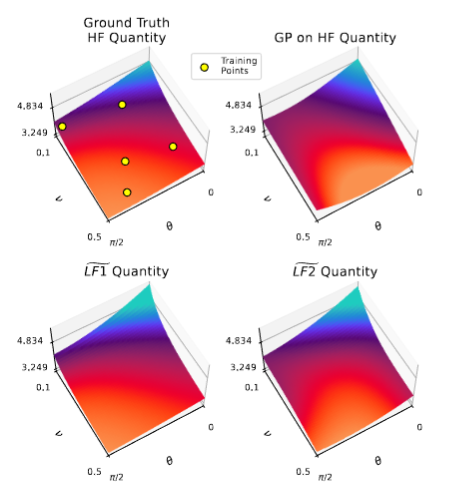 Figure 4: Model constrained GPR
Figure 4: Model constrained GPR
Table of Contents
Aims
Aims 1
Develop scalable data reduction approaches for Bayesian inverse problems.
Aims 2
Develop scalable sampling methods for large-scale Bayesian inverse solutions.
Year 1 Progress
Year 2 Progress
- Solving Bayesian Inverse Problems via Variational Autoencoders
- Deep Learning Enhanced Reduced Order Models
- Data Informed Regularization
- Autoencoder Compression
Year 3 Progress
- Autoencoder Compression
- Neural Networks and Active Subspaces
- New Approach for DNN Architecture Design
- Randomized Approaches in Scientific Computing
- Deep-learning Enhanced Model Reduction Method
- Active Subspaces for Inverse Problems
- Model Constrained DNNs for Inverse Problems
Year 4 Progress
- Autoencoder Compression
- TNet: A Tikhonov neural network for inverse problems
- A Model-Constrained Tangent Slope Learning Approach for Dynamical Systems
- Model Constrained Bayesian Neural Networks for Uncertainty Quantification
- DIAS: A Data-Informed Active Subspace Regularization Framework for Inverse Problems
- A Two-Stage Strategy for Deep Neural Network Architecture Adaptation
- A new look at the Ensemble Kalman Filter for Inverse Problems
Year 5 Progress
- Discontinuous Galerkin Network (DGNet) for Compressible Euler Equations
- Model-constrained Tikhonov Autoencoder Network (TAEN)
- Topological Derivative Approach for Architecture Design and Active Learning
- High Dimensional Linear Latent Space Approach for Stiff Systems
- Model-constrained Gaussian processes for physics- and dimension-reduction of PDEs
Undergraduate and high-school research work
- Variance Reduction-Principal Component Analysis
- Recurrent Neural Networks for Predicting ODE Dynamics
- Improving the Accuracy of Neural Networks
- Physics Informed Deep Learning Enhanced by POD
Publications
[1] Hai Van Nguyen, Jau-Uei Chen, Tan Bui-Thanh, A model-constrained discontinuous Galerkin Network (DGNet) for compressible Euler equations with out-of-distribution generalization, Computer Methods in Applied Mechanics and Engineering, Volume 440, 15 May 2025, 117912.
[2] CG Krishnanunni, Tan Bui-Thanh, An adaptive and stability-promoting layerwise training approach for sparse deep neural network architecture, Computer Methods in Applied Mechanics and Engineering, Volume 441, 1 June 2025, 117938.
[3] C G Krishnanunni, Tan Bui-Thanh, Clint Dawson. (2021). “Topological derivative approach for deep neural network architecture adaptation.” , https://arxiv.org/abs/2502.06885
[4] Hai V. Nguyen, Tan Bui-Thanh, Clint Dawson. (2025). “TAEN: A Model-Constrained Tikhonov Autoencoder Network for Forward and Inverse Problems.” , https://arxiv.org/abs/2412.07010
[5] William Cole Nockolds, C. G. Krishnanunni, Tan Bui-Thanh. (2025). “A Constant Velocity Latent Dynamics Approach for Accelerating Simulation of Stiff Nonlinear Systems.” , https://arxiv.org/abs/2501.08423
[6] Hai Nguyen, Tan Bui-Thanh. (2021). “Model-constrained Deep Learning Approaches for Inverse Problems.” , https://arxiv.org/abs/2105.12033
[7] Hai V Nguyen, Tan Bui-Thanh, A model-constrained tangent slope learning approach for dynamical systems, International Journal of Computational Fluid Dynamics, Volume 36, 2022, Issue 7.
[8] Hai Nguyen, Jonathan Wittmer, Tan Bui-Thanh. (2022). “DIAS: A Data-Informed Active Subspace Regularization Framework for Inverse Problems.” Computation, 10(3), 38.