Aim 1

We have considered both sketching (which is a relative of RMA method) and autoencoder as methods for compressing both observational and simulation data.

We have developed a streaming/online SVD approach for reducing the data dimensions. We have also developed a physics-aware autoencoder approach to compress data. We have obtained promising methods for both approaches and we are currently investigating the methods for different scenarios (type of PDEs, size of the data, the number of time steps, etc) and then wrap our results into a paper.

Aim 2

We have developed both Sinkhorn-Kropp and linear programming methods for solving the ensemble transform problems.

We have developed an adaptive tempering approach that controls the number of temperatures (and hence the number of steps) via the effective sample size.

We have investigate the influence of mutation on the performance of the methods. Our numerical results show that our sequential ensemble transform (SET) method is quite insensitive to the mutation and hence mutation does not improve the results significantly (Note that mutation is expensive, as each mutation requires Monte Carlo methods and hence more expensive forward solves). Our method thus requires essentially the same amount of work (because each optimal transport solution is negligible) of important sampling method, but our method outperforms important sampling method. In particular, while sequential important sampling method fails or performs poorly, our method is robust and yields expected results for all cases.

We have also compared our sequential ensemble transform with sequential Monte Carlo (SMC) methods, and the numerical results show that our method out-perform SMC for most cases.

We have rigorously proved that our sequential ensemble transform method (with adaptive tempering and mutation) converges. In particular, the final ensemble of particles converges weakly to the underlying posterior.

Results

We have developed a Sequential Ensemble Transform (SET) method, a new approach for generating approximate samples from a Bayesian posterior distribution. The method explores the posterior by solving a sequence of discrete linear optimal transport problems to produce a series of transport plans which map prior samples to posterior samples (see the following figure). We show that the sequence of Dirac mixture distributions produced by the SET method converges weakly to the true posterior as the sample size approaches infinity.

posterior

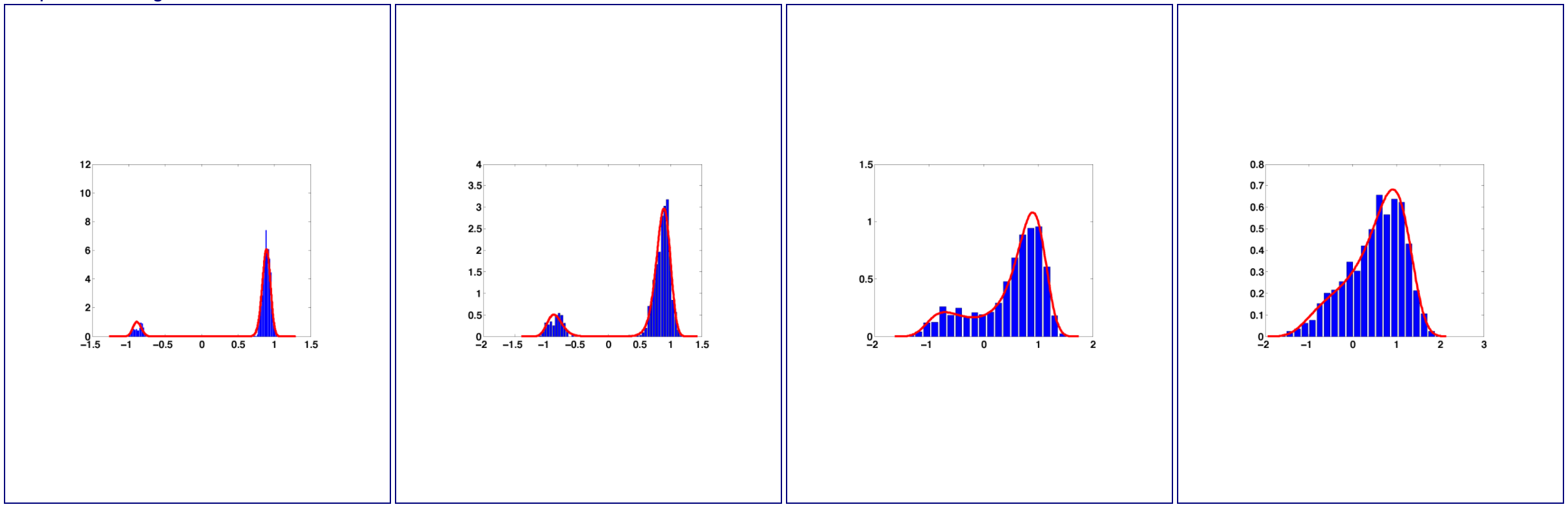
The following is the application for the ET (with the intermediate steps). The red curves are the exact solutions, and the histograms are the results from ET with 1000 particles. As can be seen, ET can map samples from single modal Gaussian distributions to nonlinear skew and multimodal distributions in one dimension.

convergence

For an open and bounded domain \(\Omega \subset \mathbb{R}^d\), with \(d \in \{1,2,3\}\), consider

\[\begin{aligned} - \nabla\cdot (e^{u} \nabla w) = 0 \qquad &\text{in} \quad \Omega \subset \mathbb{R}^{d}, \\ - e^{u} \nabla w \cdot \mathbf{n} = \textrm{Bi} \cdot w \qquad &\text{on} \quad \partial \Omega \setminus \Gamma_{R}, \\ -e^{u} \nabla w \cdot \mathbf{n} = -1 \qquad &\text{on} \quad \Gamma_{R}, \end{aligned}\]

where \(w\) is the state variable (e.g. temperature field), \(u\) the parameter of interest (e.g. logarithm of the thermal conductivity) on \(\Omega, \mathbf{n}\) the unit outward normal on \(\partial \Omega\), and \(\textrm{Bi}\) a constant (e.g. the Biot number).

The forward problem consists of computing the field \(w\) given a description of the parameter field \(u\).
The inverse problem is the task of reconstructing the field \(u\), and the associated statistical uncertainties, given some (possibly non-linear) noisy and incomplete observations of the field \(w\). Below are the results with \(500\) and \(1000\) particles in which we compute the error of the ET mean and variances for \(50\) independent runs.

ET Error The result indicates that, even without mutation, the SET method can produce a reasonable uncertainty-quantification while the adaptive SMC methodology collapses (red dots). The SMC method consistently under-estimate the uncertainty. In all settings considered, the estimations of the marginal variances is more than two orders of magnitude worse than the ones produced by the SET methodology.