Major Activities

Last year we showed that we were able to use an autoencoder to compress the state solutions of a time-dependent PDE, u(t), significantly saving on storage cost, and then retrieve these solutions by passing the compessed state through the decoder portion with high accuracy (5% average relative error). The reason for compressing is to eliminate the need for a checkpointing strategy when solving a PDE constrained inverse problem where the time-dependent PDE would need to be solved again each time the state is needed due to memory constraints, an expensive proposition. This year we showed that such an autoencoder compression strategy is indeed a viable alternative to the checkpointing strategy, resulting in inverse solutions that have minimal degradation due to perturbations in the state due to compression losses and that the cost of compression/decompression is lower than the cost of additional solves of the PDE for well-chosen neural network architectures. For a Gauss-Newton optimization method, the compressed states are used in each of the adjoint, incremental forward, and incremental adjoint PDE solves, resulting in significant time-savings over the course of solving the inverse problem.

One particular advantage of this method is that it scales perfectly. The proposed method holds the local (per MPI rank) problem size constant and assigns one instance of the autoencoder to each MPI rank with no communication between ranks required to compress/decompress. Such a strategy makes this method particularly effective on large problems as the cost of recomputing the PDE solution becomes increasingly dominated by communication costs.

Significant Results

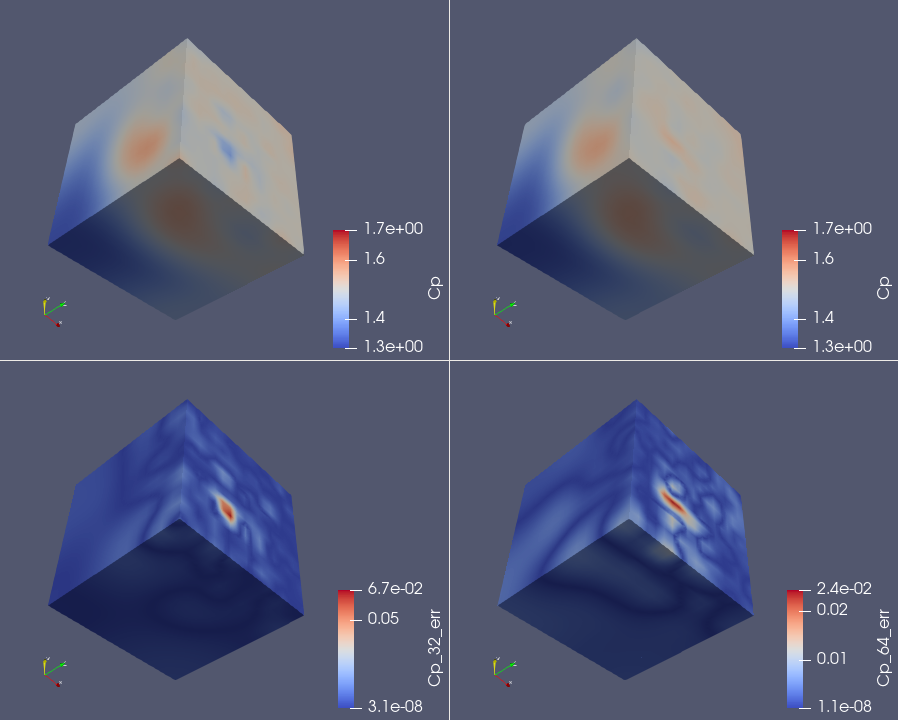
acoustic-elastic wave equation video

Relative error of the parameter of interest Cp for two different compression levels. The local state size is 4096 and compressed size is 32 (left) and 64 (right). This is equivalent to a compression level of 128x and 64x, respectively. The top row shows the predicted value of Cp and the bottom row shows the relative error. The average relative error is 0.2% with 128x compression and 0.1% with 64x compression. In this example, there were 64 MPI ranks, leading to a total state size of 262,144. Using GPU, we get a 40% speedup over recomputing the forward solution and 10% speedup when using CPU only.